Question

【題目】已知傾斜角為的直線經過拋物線：的焦點，與拋物線相交于、兩點，且.

（Ⅰ）求拋物線的方程；

（Ⅱ）過點的兩條直線、分別交拋物線于點、和、，線段和的中點分別為、.如果直線與的傾斜角互余，求證：直線經過一定點.

Answer 1

【答案】（Ⅰ）；（2）

【解析】試題分析：

（Ⅰ）設出直線的方程為，與拋物線方程聯立消元后可得，結合拋物線的定義及條件可得，故拋物線的方程為．（Ⅱ）設直線的斜率為，則由條件可得直線的斜率為，由直線與拋物線的交點可得點，同理點，故，于是可得直線MN的方程為，可得直線過定點．

試題解析：

（Ⅰ）由題意可設直線的方程為，

由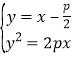消去y整理得，

設令，，

則，

由拋物線的定義得，

∴，

∴.

∴拋物線的方程為.

（Ⅱ）設直線、的傾斜角分別為、，直線的斜率為，則.

∵直線與的傾斜角互余，

∴ ，

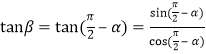
∴直線的斜率為.

∴直線的方程為，即，

由消去x整理得，

∴，

∴，

∴點，

以代替點M坐標中的，可得點，

∴ .

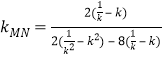
∴直線的方程為，

即，

顯然當，.

∴直線經過定點.