
拋物線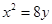 的準線與
的準線與 軸交于點
軸交于點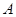 ,點
,點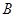 在拋物線對稱軸上,過
在拋物線對稱軸上,過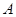 可作直線交拋物線于點
可作直線交拋物線于點 、
、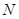 ,使得
,使得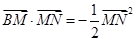 ,則
,則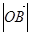 的取值范圍是 .
的取值范圍是 .
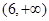
解析試題分析:由題意可得A(0,-2),直線MN的斜率k存在且k≠0,
設直線MN的方程為y=kx-2,聯立方程組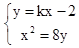 ,得x2-8kx+16=0,
,得x2-8kx+16=0,
設M (x1,x2),N(x2,y2),MN 的中點E(x0,y0),
則△=64k2-64>0,即k2>1,
x1+x2=8k,y1+y2=k(x1+x2)-4=-4+8k2,
∴x0=4k,y0=-2+4k2即E(4k,-2+4k2).
∵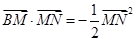 ,
,
∴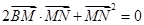 ,即
,即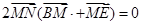 ,而
,而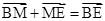 ,
,
∴BE⊥MN即點B在MN的垂直平分線上,
∵MN的斜率為k,E(4k,-2+4k2).
∴MN的垂直平分線BE的方程為:y-4k2+2=-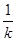 (x-4k),與y軸的交點即是B,
(x-4k),與y軸的交點即是B,
令x=0可得,y=2+4k2,
則|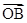 |=2+4k2>6.
|=2+4k2>6.
故答案為(6,+∞).
考點:本題主要考查平面向量的線性運算、數量積,直線與拋物線的位置關系。
點評:中檔題,本題主要考查了平面向量的線性運算、數量積,直線與拋物線的位置關系。在研究過程中運用方程的根與系數關系,使問題得到簡化。


 期末沖刺100分創(chuàng)新金卷完全試卷系列答案
期末沖刺100分創(chuàng)新金卷完全試卷系列答案國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com