
【題目】對于函數y=3sin(2x + ![]() )
)
(1)求最小正周期、對稱軸和對稱中心;
(2)簡述此函數圖象是怎樣由函數y=sinx的圖象作變換得到的.
【答案】(1)![]() ,
, ![]() ,
, ![]() (2)見解析
(2)見解析
【解析】試題分析:(1)根據正弦函數對應性質: ![]() 求最小正周期、對稱軸和對稱中心(2)正弦函數圖像變換,分振幅、相位、伸縮三種,注意相位變換時是對x而言
求最小正周期、對稱軸和對稱中心(2)正弦函數圖像變換,分振幅、相位、伸縮三種,注意相位變換時是對x而言
試題解析:解:(1)對于函數y=3sin(2x+![]() ),最小正周期為
),最小正周期為![]() =π.
=π.
對于函數y=![]() sin(2x+
sin(2x+![]() )﹣1,令2x+
)﹣1,令2x+![]() =kπ+
=kπ+![]() ,k∈Z,
,k∈Z,
解得x=![]() +
+![]() ,k∈Z,故函數的對稱軸方程為x=
,k∈Z,故函數的對稱軸方程為x=![]() +
+![]() ,k∈Z,
,k∈Z,
令2x+![]() =kπ,k∈Z,解得x=
=kπ,k∈Z,解得x=![]() ﹣
﹣![]() ,k∈Z,
,k∈Z,
故函數的對稱中心是(![]() ﹣
﹣![]() ,0),k∈Z.
,0),k∈Z.
(2)把函數y=sinx的圖象向左平移![]() 個單位,可得y=sin(x+
個單位,可得y=sin(x+![]() )的圖象;
)的圖象;
再把橫坐標變為原來的![]() 倍,可得y=sin(2x+
倍,可得y=sin(2x+![]() )的圖象;
)的圖象;
再把縱坐標變為原來的3倍,可得y=3sin(2x+![]() )的圖象.
)的圖象.


 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源: 題型:
【題目】在經濟學中,函數f(x)的邊際函數為Mf(x),定義為Mf(x)=f(x+1)﹣f(x).已知某服裝公司每天最多
生產100件.生產x件的收入函數為R(x)=300x﹣2x2(單位元),其成本函數為C(x)=50x+300(單位:元),利潤等于收入與成本之差.
(1)求出利潤函數p(x)及其邊際利潤函數Mp(x);
(2)分別求利潤函數p(x)及其邊際利潤函數Mp(x)的最大值;
(3)你認為本題中邊際利潤函數Mp(x)最大值的實際意義是什么?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知右焦點為F(c,0)的橢圓M: ![]() =1(a>b>0)過點
=1(a>b>0)過點 ![]() ,且橢圓M關于直線x=c對稱的圖形過坐標原點.
,且橢圓M關于直線x=c對稱的圖形過坐標原點.
(1)求橢圓M的方程;
(2)過點(4,0)且不垂直于y軸的直線與橢圓M交于P,Q兩點,點Q關于x軸的對稱原點為E,證明:直線PE與x軸的交點為F.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=﹣x2+ax+4,g(x)=|x+1|+|x﹣1|.
(1)當a=1時,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[﹣1,1],求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】阿波羅尼斯是古希臘著名數學家,與歐幾里得、阿基米德被稱為亞歷山大時期數學三巨匠,他對圓錐曲線有深刻而系統的研究,主要研究成果集中在他的代表作《圓錐曲線》一書,阿波羅尼斯圓是他的研究成果之一,指的是:已知動點M與兩定點A、B的距離之比為λ(λ>0,λ≠1),那么點M的軌跡就是阿波羅尼斯圓.下面,我們來研究與此相關的一個問題.已知圓:x2+y2=1和點 ![]() ,點B(1,1),M為圓O上動點,則2|MA|+|MB|的最小值為( )
,點B(1,1),M為圓O上動點,則2|MA|+|MB|的最小值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某租賃公司擁有汽車100輛.當每輛車的月租金為![]() 元時,可全部租出.當每輛車的月租金每增加50元時,未租出的車將會增加一輛.租出的車每輛每月需要維護費150元,未租出的車每輛每月需要維護費50元.若使租賃公司的月收益最大,每輛車的月租金應該定為__________.
元時,可全部租出.當每輛車的月租金每增加50元時,未租出的車將會增加一輛.租出的車每輛每月需要維護費150元,未租出的車每輛每月需要維護費50元.若使租賃公司的月收益最大,每輛車的月租金應該定為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖, ![]() 是圓柱的母線,
是圓柱的母線, ![]() 是
是![]() 的直徑,
的直徑, ![]() 是底面圓周上異于
是底面圓周上異于![]() 的任意一點,
的任意一點, ![]() ,
, ![]() .
.
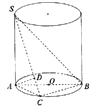
(1)求證: ![]()
(2)當三棱錐![]() 的體積最大時,求
的體積最大時,求![]() 與平面
與平面![]() 所成角的大小;
所成角的大小;
(3)![]() 上是否存在一點
上是否存在一點![]() ,使二面角
,使二面角![]() 的平面角為45°?若存在,求出此時
的平面角為45°?若存在,求出此時![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com