
【題目】已知橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
, ![]() ,點
,點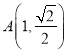 在橢圓
在橢圓![]() 上.
上.
(Ⅰ)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(Ⅱ)是否存在斜率為2的直線![]() ,使得當(dāng)直線
,使得當(dāng)直線![]() 與橢圓
與橢圓![]() 有兩個不同交點
有兩個不同交點![]() 、
、![]() 時,能在直線
時,能在直線![]() 上找到一點
上找到一點![]() ,在橢圓
,在橢圓![]() 上找到一點
上找到一點![]() ,滿足
,滿足![]() ?若存在,求出直線
?若存在,求出直線![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】劉老師是一位經(jīng)驗豐富的高三理科班班主任,經(jīng)長期研究,他發(fā)現(xiàn)高中理科班的學(xué)生的數(shù)學(xué)成績(總分150分)與理綜成績(物理、化學(xué)與生物的綜合,總分300分)具有較強(qiáng)的線性相關(guān)性,以下是劉老師隨機(jī)選取的八名學(xué)生在高考中的數(shù)學(xué)得分x與理綜得分y(如下表):
學(xué)生編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
數(shù)學(xué)分?jǐn)?shù)x | 52 | 64 | 87 | 96 | 105 | 123 | 132 | 141 |
理綜分?jǐn)?shù)y | 112 | 132 | 177 | 190 | 218 | 239 | 257 | 275 |
參考數(shù)據(jù)及公式: ![]() .
.
(1)求出y關(guān)于x的線性回歸方程;
(2)若小汪高考數(shù)學(xué)110分,請你預(yù)測他理綜得分約為多少分?(精確到整數(shù)位);
(3)小金同學(xué)的文科一般,語文與英語一起能穩(wěn)定在215分左右.如果他的目標(biāo)是在
高考總分沖擊600分,請你幫他估算他的數(shù)學(xué)與理綜大約分別至少需要拿到多少分?(精確到整數(shù)位).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
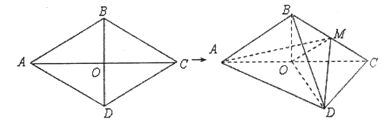
【題目】如圖,棱形![]() 的邊長為6,
的邊長為6, ![]() ,
,![]() .將棱形
.將棱形![]() 沿對角線
沿對角線![]() 折起,得到三棱錐
折起,得到三棱錐![]() ,點
,點![]() 是棱
是棱![]() 的中點,
的中點, ![]() .
.
(Ⅰ)求證:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】衡州市臨棗中學(xué)高二某小組隨機(jī)調(diào)查芙蓉社區(qū)160個人,以研究這一社區(qū)居民在20:00-22:00時間段的休閑方式與性別的關(guān)系,得到下面的數(shù)據(jù)表:
休閑方式 性別 | 看電視 | 看書 | 合計 |
男 | 20 | 100 | 120 |
女 | 20 | 20 | 40 |
合計 | 40 | 120 | 160 |
下面臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
(Ⅰ)將此樣本的頻率估計為總體的概率,隨機(jī)調(diào)查3名在該社區(qū)的男性,設(shè)調(diào)查的3人在這一時間段以看書為休閑方式的人數(shù)為隨機(jī)變量![]() ,求
,求![]() 的分別列和期望;
的分別列和期望;
(Ⅱ)根據(jù)以上數(shù)據(jù),能否有99%的把握認(rèn)為“在20:00-22:00時間段的休閑方式與性別有關(guān)系”?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了解某單位員工的月工資水平,從該單位500位員工中隨機(jī)抽取了50位進(jìn)行調(diào)查,得到如下頻數(shù)分布表和頻率分布直方圖:
月工資 (單位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
男員工數(shù) | 1 | 8 | 10 | 6 | 4 | 4 |
女員工數(shù) | 4 | 2 | 5 | 4 | 1 | 1 |
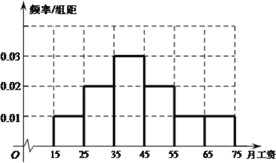
(1)![]() 試由上圖估計該單位員工月平均工資;
試由上圖估計該單位員工月平均工資;
(2)現(xiàn)用分層抽樣的方法從月工資在![]() 和
和![]() 的兩組所調(diào)查的男員工中隨機(jī)選取5人,問各應(yīng)抽取多少人?
的兩組所調(diào)查的男員工中隨機(jī)選取5人,問各應(yīng)抽取多少人?
(3)若從月工資在![]() 和
和![]() 兩組所調(diào)查的女員工中隨機(jī)選取2人,試求這2人月工資差不超過1000元的概率.
兩組所調(diào)查的女員工中隨機(jī)選取2人,試求這2人月工資差不超過1000元的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列{an}的前n項和為Sn=2n2,{bn}為等比數(shù)列,且a1=b1,b2(a2-a1)=b1.
(1)求數(shù)列{an}和{bn}的通項公式;
(2)設(shè)cn=![]() ,求數(shù)列{cn}的前n項和Tn.
,求數(shù)列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]() .
.
(1)當(dāng)![]() 時,求
時,求![]() 在區(qū)間
在區(qū)間![]() 上的最值;
上的最值;
(2)討論![]() 的單調(diào)性;
的單調(diào)性;
(3)當(dāng)![]() 時,有
時,有![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() ,
,![]() 是橢圓
是橢圓![]() 的右焦點,直線
的右焦點,直線![]() 的斜率為
的斜率為![]() ,
,![]() 為坐標(biāo)原點.
為坐標(biāo)原點.
(1)求![]() 的方程;
的方程;
(2)設(shè)過點![]() 的動直線
的動直線![]() 與
與![]() 相交于
相交于![]() 兩點,問:是否存在直線
兩點,問:是否存在直線![]() ,使以
,使以![]() 為直徑的圓經(jīng)過原點
為直徑的圓經(jīng)過原點![]() ,若存在,求出對應(yīng)直線
,若存在,求出對應(yīng)直線![]() 的方程,若不存在,請說明理由.
的方程,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)舉行了一次“環(huán)保知識競賽”, 全校學(xué)生參加了這次競賽.為了了解本次競賽成績情況,從中抽取了部分學(xué)生的成績(得分取正整數(shù),滿分為100分)作為樣本進(jìn)行統(tǒng)計.請根據(jù)下面尚未完成并有局部污損的頻率分布表和頻率分布直方圖(如圖所示)解決下列問題:
![]()
| 分組 | 頻數(shù) | 頻率 |
第1組 | [50,60) | 8 | 0 16 |
第2組 | [60,70) | a | ▓ |
第3組 | [70,80) | 20 | 0 40 |
第4組 | [80,90) | ▓ | 0 08 |
第5組 | [90,100] | 2 | b |
合計 | ▓ | ▓ |

(1)求出![]() 的值;
的值;
(2)在選取的樣本中,從競賽成績是80分以上(含80分)的同學(xué)中隨機(jī)抽取2名同學(xué)到廣場參加環(huán)保知識的志愿宣傳活動
(ⅰ)求所抽取的2名同學(xué)中至少有1名同學(xué)來自第5組的概率;
(ⅱ)求所抽取的2名同學(xué)來自同一組的概率
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com