
【題目】已知全集U=R,函數y= ![]() +
+ ![]() 的定義域為A,函數y=
的定義域為A,函數y= ![]() 的定義域為B.
的定義域為B.
(1)求集合A、B.
(2)(UA)∪(UB).
【答案】
(1)解:由 ![]() x≥2
x≥2
A={x|x≥2}
由 ![]() x≥﹣2且x≠3
x≥﹣2且x≠3
B={x|x≥﹣2且x≠3}
(2)解:A∩B={x|x≥2且x≠3}
∴(CUA)∪(CUB)=CU(A∩B)={x|x<2或x=3}
【解析】(1)根據負數沒有平方根及分母不為零列出不等式組,求出不等式組的解集確定出集合A,B.(2)先利用(CUA)(CUB)=CU(A∩B),再結合所求出的集合利用交集的定義即可得到(CUA)∪(CUB).
【考點精析】本題主要考查了交、并、補集的混合運算和函數的定義域及其求法的相關知識點,需要掌握求集合的并、交、補是集合間的基本運算,運算結果仍然還是集合,區分交集與并集的關鍵是“且”與“或”,在處理有關交集與并集的問題時,常常從這兩個字眼出發去揭示、挖掘題設條件,結合Venn圖或數軸進而用集合語言表達,增強數形結合的思想方法;求函數的定義域時,一般遵循以下原則:①![]() 是整式時,定義域是全體實數;②
是整式時,定義域是全體實數;②![]() 是分式函數時,定義域是使分母不為零的一切實數;③
是分式函數時,定義域是使分母不為零的一切實數;③![]() 是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零才能正確解答此題.
是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|< ![]() )的最小正周期為2 π,最小值為﹣2,且當x=
)的最小正周期為2 π,最小值為﹣2,且當x= ![]() 時,函數取得最大值4. (I)求函數 f(x)的解析式;
時,函數取得最大值4. (I)求函數 f(x)的解析式;
(Ⅱ)求函數f(x)的單調遞增區間;
(Ⅲ)若當x∈[ ![]() ,
, ![]() ]時,方程f(x)=m+1有解,求實數m的取值范圍.
]時,方程f(x)=m+1有解,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“a≥3 ![]() ”是“直線l:2ax﹣y+2a2=0(a>0)與雙曲線C:
”是“直線l:2ax﹣y+2a2=0(a>0)與雙曲線C: ![]() ﹣
﹣ ![]() =1的右支無交點”的( )
=1的右支無交點”的( )
A.充分不必要條件
B.必要不充分條件
C.充要條件
D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}滿足an+1+an=4n﹣3(n∈N*)
(Ⅰ)若{an}是等差數列,求其通項公式;
(Ⅱ)若{an}滿足a1=2,Sn為{an}的前n項和,求S2n+1 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知直三棱柱ABC﹣A1B1C1中,AB=5,AC=4,BC=3,AA1=4,點D在AB上. 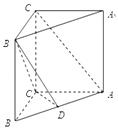
(1)若D是AB中點,求證:AC1∥平面B1CD;
(2)當 ![]() =
= ![]() 時,求二面角B﹣CD﹣B1的余弦值.
時,求二面角B﹣CD﹣B1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() :
: ![]() ,其左右焦點為
,其左右焦點為![]()
![]() 及
及![]() ,過點
,過點![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() ,
, ![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,
, ![]() 的中垂線與
的中垂線與![]() 軸和
軸和![]() 軸分別交于
軸分別交于![]() ,
, ![]() 兩點,且
兩點,且![]() 、
、![]() 、
、![]() 構成等差數列.
構成等差數列.
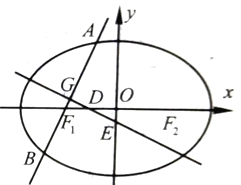
(1)求橢圓![]() 的方程;
的方程;
(2)記![]() 的面積為
的面積為![]() ,
, ![]() (
(![]() 為原點)的面積為
為原點)的面積為![]() .試問:是否存在直線
.試問:是否存在直線![]() ,使得
,使得![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的一條對稱軸為
的一條對稱軸為![]() ,且最高點的縱坐標是
,且最高點的縱坐標是![]() .
.
(1)求![]() 的最小值及此時函數
的最小值及此時函數![]() 的最小正周期、初相;
的最小正周期、初相;
(2)在(1)的情況下,設![]() ,求函數
,求函數![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com