【題目】在正方體
中， 
、
分別是
、
的中點.
(1)求證：四邊形
是菱形；
(2)求異面直線
與
所成角的大小 (結果用反三角函數值表示) .
【答案】(1)證明見解析；（2）
.
【解析】試題分析：（1）建立空間直角坐標系，如圖所示：先證其是平行四邊形，再根據空間向量模相等說明鄰邊相等即可；（2）可得
，利用空間向量夾角余弦公式可得結果.
試題解析：（1）設正方體的棱長為1，建立空間直角坐標系，如圖所示：
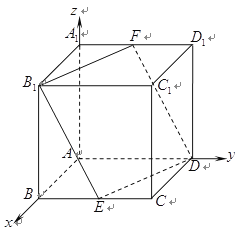
則
, 
, 
, 
,
所以
,即
且
,故四邊形
是平行四邊形
又因為
,所以
故平行四邊形
是菱形
(2)因為
設異面直線
與
所成的角的大小為
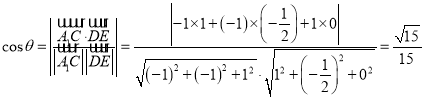
所以
, 故異面直線
與
所成的角的大小為
.
【方法點晴】本題主要考查異面直線所成的角以及空間向量的應用，屬于難題.求異面直線所成的角主要方法有兩種：一是向量法，根據幾何體的特殊性質建立空間直角坐標系后，分別求出兩直線的方向向量，再利用空間向量夾角的余弦公式求解；二是傳統法，利用平行四邊形、三角形中位線等方法找出兩直線成的角，再利用平面幾何性質求解.
作業輔導系列答案
同步學典一課多練系列答案
經典密卷系列答案
金牌課堂練系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓E：
=1（a＞b＞0）的焦距為2
， 且該橢圓經過點(,
)．
（Ⅰ）求橢圓E的方程；
（Ⅱ）經過點P（﹣2，0）分別作斜率為k1 ， k2的兩條直線，兩直線分別與橢圓E交于M，N兩點，當直線MN與y軸垂直時，求k1k2的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某車間為了規定工時定額，需要確定加工某零件所花費的時間，為此做了四次實驗，得到的數據如表：
零件的個數x（個） | 2 | 3 | 4 | 5 |
加工的時間y（小時） | 2.5 | 3 | 4 | 4.5 |
（1）在給定的坐標系中畫出表中數據的散點圖；
（2）求出y關于x的線性回歸方程y= 
x+ 
，并在坐標系中畫出回歸直線；
（3）試預測加工6個零件需要多少時間？
（注： = 
， = 
﹣ 
）
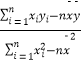查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設命題p：實數x滿足x2﹣4ax+3a2＜0，其中a＞0，命題q：實數x滿足
．
（Ⅰ）若a=1，且p∧q為真，求實數x的取值范圍；
（Ⅱ）若￢p是￢q的充分不必要條件，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=lnx+2sinα（α∈（0，
））的導函數f′（x），若存在x0＜1使得f′（x0）=f（x0）成立，則實數α的取值范圍為（ ）
A.（
， ）
B.（0，）
C.（
， ）
D.（0，）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
(其中
， 
).
(1)若函數
在
上為增函數，求實數
的取值范圍；
(2)當
時，求函數
在
上的最大值和最小值；
(3)當
時，求證：對于任意大于1的正整數
，都有
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的中心在原點，焦點在
軸上，離心率
．以兩個焦點和短軸的兩個端點為頂點的四邊形的周長為8，面積為
．
（Ⅰ）求橢圓
的方程；
（Ⅱ）若點
為橢圓
上一點，直線
的方程為
，求證：直線
與橢圓
有且只有一個交點．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖莖葉圖記錄了甲、乙兩組各四名同學的植樹棵數．乙組記錄中有一個數據模糊，無法確認，在圖中以Z表示．
（1）如果Z=8，求乙組同學植樹棵數的平均數和方差；
（2）如果Z=9，分別從甲、乙兩組中隨機選取一名同學，求這兩名同學的植樹總棵數為19的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
