
【題目】已知![]() (
(![]() 為常數).
為常數).
(1)當![]() 時,求函數
時,求函數![]() 的單調性;
的單調性;
(2)當![]() 時,求證:
時,求證: ![]() ;
;
(3)試討論函數![]() 零點的個數.
零點的個數.
【答案】(1)![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減(2)見解析(3)見解析
上單調遞減(2)見解析(3)見解析
【解析】試題分析:(1)將參數值代入得到函數表達式,求導研究導函數的正負即可;(2)記![]() ,由題意即證,當
,由題意即證,當![]() 時,
時, ![]() ,對函數求導研究單調性求最值即可;(3)直接對函數求導,研究函數的單調性,得到函數的變化趨勢,結合圖像討論函數的零點個數。
,對函數求導研究單調性求最值即可;(3)直接對函數求導,研究函數的單調性,得到函數的變化趨勢,結合圖像討論函數的零點個數。
解析:
(1)解當![]() 時,
時, ![]() ,所以
,所以![]() (
(![]() ),
),
當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ;
;
故![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(2)證明:記![]() ,
,
由題意即證,當![]() 時,
時, ![]() .
.
又![]() (
(![]() ),
),
記![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上恒成立,則
上恒成立,則![]() 在
在![]() 上單調遞減,
上單調遞減,
![]() ,即證.
,即證.
(3)由題意,  (
(![]() ).
).
①若![]() ,則
,則![]() ,故
,故![]() 在
在![]() 上單調遞增,
上單調遞增,
又因為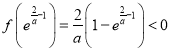 ,且
,且![]() ,
,
由零點存在性定理知, ![]() 在
在![]() 上有且只有一個零點.
上有且只有一個零點.
②若![]() ,當
,當![]() ,
, ![]() ,則
,則![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() ,
, ![]() ,則
,則![]() 在
在![]() 上單調遞減,
上單調遞減,
所以, ![]() 是
是![]() 在
在![]() 上的極大值點,也是最大值點,
上的極大值點,也是最大值點, ![]() .
.
(i)當![]() ,即
,即![]() ,
, ![]() 恒成立,則
恒成立,則![]() 在
在![]() 上無零點;
上無零點;
(ii)當![]() ,即
,即![]() ,
, ![]() ,則
,則![]() 在
在![]() 上有一個零點;
上有一個零點;
(iii)當![]() ,即
,即![]() ,
, ![]() ,
,
而當![]() 時,有
時,有![]() ,理由如下:令
,理由如下:令![]() (
(![]() ),則
),則![]() ,
,
所以![]() 在
在![]() 上單調遞增,
上單調遞增, ![]() ,即
,即![]() .
.
![]() ,由(2)知
,由(2)知![]() ,而
,而![]() ,
,
由![]() 在
在![]() 上的單調性及零點存在性定理可知,
上的單調性及零點存在性定理可知, ![]() 分別在
分別在![]() 和
和![]() 上各有一個零點,即
上各有一個零點,即![]() 在
在![]() 上有兩個零點.
上有兩個零點.
綜上所述,當![]() 或
或![]() 時,
時, ![]() 在
在![]() 上有一個零點;
上有一個零點;
當![]() 時,
時, ![]() 在
在![]() 上有兩個零點;
上有兩個零點;
當![]() 時,
時, ![]() 在
在![]() 上沒有零點..
上沒有零點..


科目:高中數學 來源: 題型:
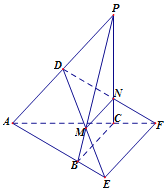
【題目】如圖,在三棱錐![]() 中,
中, ![]() 兩兩垂直且相等,過
兩兩垂直且相等,過![]() 的中點
的中點![]() 作平面
作平面![]() ∥
∥![]() ,且
,且![]() 分別交PB,PC于M、N,交
分別交PB,PC于M、N,交![]() 的延長線于
的延長線于![]() .
.
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知復數z=![]() ,(m∈R,i是虛數單位).
,(m∈R,i是虛數單位).
(1)若z是純虛數,求m的值;
(2)設![]() 是z的共軛復數,復數
是z的共軛復數,復數![]() +2z在復平面上對應的點在第一象限,求m的取值范圍.
+2z在復平面上對應的點在第一象限,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() ,且離心率為
,且離心率為![]() .
.
(![]() )求橢圓
)求橢圓![]() 的方程.
的方程.
(![]() )已知雙曲線
)已知雙曲線![]() 的離心率是橢圓
的離心率是橢圓![]() 的離心率的倒數,其頂點為橢圓的焦點,求雙曲線
的離心率的倒數,其頂點為橢圓的焦點,求雙曲線![]() 的方程.
的方程.
(![]() )設直線
)設直線![]() 與雙曲線交于
與雙曲線交于![]() ,
, ![]() 兩點,過
兩點,過![]() 的直線
的直線![]() 與線段
與線段![]() 有公共點,求直線
有公共點,求直線![]() 的傾斜角的取值范圍.
的傾斜角的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學對男女學生是否喜愛古典音樂進行了一個調查,調查者對學校高三年級隨機抽取了100名學生,調查結果如表:
喜愛 | 不喜愛 | 總計 | |
男學生 | 60 | 80 | |
女學生 | |||
總計 | 70 | 30 |
附:K2= ![]()
P(K2≥k0) | 0.100 | 0.050 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
(1)完成如表,并根據表中數據,判斷是否有95%的把握認為“男學生和女學生喜歡古典音樂的程度有差異”;
(2)從以上被調查的學生中以性別為依據采用分層抽樣的方式抽取10名學生,再從這10名學生中隨機抽取5名學生去某古典音樂會的現場觀看演出,求正好有X個男生去觀看演出的分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示是某條公共汽車路線收支差額y與乘客量x的圖象(收支差額=車票收入—支出費用)由于目前本條線路在虧損,公司有關人員提出了兩條建議:
建議(Ⅰ)是不改變車票價格,減少支出費用;建議(Ⅱ)是不改變支出費用,提高車票價格. 圖中虛線表示調整前的狀態,實線表示調整后的狀態. 在上面四個圖象中
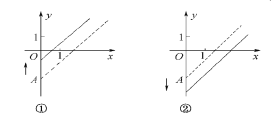
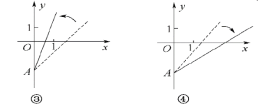
A. ①反映了建議(Ⅱ),③反映了建議(Ⅰ) B. ①反映了建議(Ⅰ),③反映了建議(Ⅱ)
C. ②反映了建議(Ⅰ),④反映了建議(Ⅱ) D. ④反映了建議(Ⅰ),②反映了建議(Ⅱ)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】微信支付誕生于微信紅包,早期知識作為社交的一部分“發紅包”而誕生的,在發紅包之余才發現,原來微信支付不僅可以用來發紅包,還可以用來支付,現在微信支付被越來越多的人們所接受,現從某市市民中隨機抽取300為對是否使用微信支付進行調查,得到下列![]() 的列聯表:
的列聯表:
年輕人 | 非年輕人 | 總計 | |
經常使用微信支付 | 165 | 225 | |
不常使用微信支付 | |||
合計 | 90 | 300 |
根據表中數據,我們得到的統計學的結論是:由__________的把握認為“使用微信支付與年齡有關”。
|
|
|
|
|
|
|
|
|
|
|
|
其中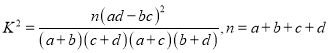
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 在定義域內為增函數,求實數
在定義域內為增函數,求實數![]() 的取值范圍;
的取值范圍;
(2)在(1)的條件下,若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的極小值;
的極小值;
(3)設![]() ,
, ![]() .若函數
.若函數![]() 存在兩個零點
存在兩個零點![]() ,且滿足
,且滿足![]() ,問:函數
,問:函數![]() 在
在![]() 處的切線能否平行于
處的切線能否平行于![]() 軸?若能,求出該切線方程,若不能,請說明理由.
軸?若能,求出該切線方程,若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com