
(09年海淀區(qū)期中理)(14分)
某中學(xué)已選派20名學(xué)生觀看當(dāng)?shù)嘏e行的三場(chǎng)(同時(shí)進(jìn)行)比賽,名額分配如下:
足球 | 跳水 | 柔道 |
10 | 6 | 4 |
(Ⅰ)從觀看比賽的學(xué)生中任選2名,求他們觀看的恰好是同一場(chǎng)比賽的概率;
(Ⅱ)從觀看比賽的學(xué)生中,任選3人,求他們中至少有1人觀看的是足球比賽的概率;
(Ⅲ) 如果該中學(xué)可以再安排4名教師選擇觀看上述3場(chǎng)比賽(假設(shè)每名教師選擇觀看各場(chǎng)比賽是等可能的,且各位教師的選擇是相互獨(dú)立的),記觀看足球比賽的教師人數(shù)為![]() ,求隨機(jī)變量
,求隨機(jī)變量![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
解析:(Ⅰ)設(shè)從觀看比賽的學(xué)生中任選2人,他們恰好觀看同一場(chǎng)比賽的事件為![]() .
.
則![]() .……………………3分
.……………………3分
答:從觀看比賽的學(xué)生中任選2人,他們恰好觀看的是同一場(chǎng)比賽的概率是![]() .
.
(Ⅱ)解法1:設(shè)所選的3名學(xué)生均沒有觀看過足球比賽為事件B.……4分
則![]() ,所以
,所以![]() .……………………7分
.……………………7分
答:從觀看比賽的學(xué)生中任選3人,他們中至少有1人觀看的是足球比賽的概率是![]() .
.
解法2:設(shè)從觀看比賽的學(xué)生中任選3人,他們中至少有1人觀看的是足球比賽的事件為C.…………4分
則![]() …………………………7分]
…………………………7分]
答:從觀看比賽的學(xué)生中任選3人,他們中至少有1人觀看的是足球比賽的概率是![]() .
.
(Ⅲ)解法1:![]() 的所有取值為0,1,2,3,4.…………………………8分
的所有取值為0,1,2,3,4.…………………………8分
由題意可知,每位教師觀看足球比賽的概率均為![]() .…………………………9分
.…………………………9分
所以![]() ;
; 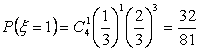 ;
;
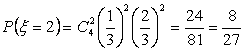 ;
;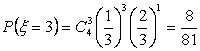 ;
;
![]() ………………………………11分
………………………………11分
隨機(jī)變量![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
………………12分
所以![]() .……………14分
.……………14分
解法2:由題意可知,每位教師觀看足球比賽的概率均為![]() .………………8分
.………………8分
則隨機(jī)變量![]() ~B(4,
~B(4,![]() )……………………………………10分
)……………………………………10分
所以隨機(jī)變量![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
……………12分
所以![]() .………………………14分
.………………………14分


 一諾書業(yè)暑假作業(yè)快樂假期云南美術(shù)出版社系列答案
一諾書業(yè)暑假作業(yè)快樂假期云南美術(shù)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(09年海淀區(qū)期中理)(14分)
設(shè)![]() 是定義在區(qū)間D上的函數(shù),若對(duì)任何實(shí)數(shù)
是定義在區(qū)間D上的函數(shù),若對(duì)任何實(shí)數(shù)![]() 以及D中的任意兩數(shù)
以及D中的任意兩數(shù)![]() ,恒有
,恒有![]() ,則稱
,則稱![]() 為定義在D上的C函數(shù).
為定義在D上的C函數(shù).
(Ⅰ)試判斷函數(shù)![]() ,
,![]() 是否為各自定義域上的C函數(shù),并說明理由;
是否為各自定義域上的C函數(shù),并說明理由;
(Ⅱ)已知![]() 是R上的C函數(shù),m是給定的正整數(shù),設(shè)
是R上的C函數(shù),m是給定的正整數(shù),設(shè)![]() ,且
,且![]() ,記
,記![]() . 對(duì)于滿足條件的任意函數(shù)
. 對(duì)于滿足條件的任意函數(shù)![]() ,試求
,試求![]() 的最大值;
的最大值;
(Ⅲ)若![]() 是定義域?yàn)?B>R的函數(shù),且最小正周期為
是定義域?yàn)?B>R的函數(shù),且最小正周期為![]() ,試證明
,試證明![]() 不是R上的C函數(shù).
不是R上的C函數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(09年海淀區(qū)期中理)(14分)
設(shè)函數(shù)![]()
![]() .
.
(Ⅰ)當(dāng)![]() 且函數(shù)
且函數(shù)![]() 在其定義域上為增函數(shù)時(shí),求
在其定義域上為增函數(shù)時(shí),求![]() 的取值范圍;
的取值范圍;
(Ⅱ)若函數(shù)![]() 在
在![]() 處取得極值,試用
處取得極值,試用![]() 表示
表示![]() ;
;
(Ⅲ)在(Ⅱ)的條件下,討論函數(shù)![]() 的單調(diào)性.
的單調(diào)性.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(09年海淀區(qū)期中理)(13分)
已知函數(shù)![]() ,把函數(shù)
,把函數(shù)![]() 的圖象向左平移一個(gè)單位得到函數(shù)
的圖象向左平移一個(gè)單位得到函數(shù)![]() 的圖象,且
的圖象,且![]() 是偶函數(shù).
是偶函數(shù).
(Ⅰ) 求![]() 的值;
的值;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(09年海淀區(qū)期中理)(12分)
已知關(guān)于x的不等式組 ,其中
,其中![]() .
.
(Ⅰ)求不等式①的解集;
(Ⅱ)若不等式組的解集為空集,求實(shí)數(shù)查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com