
【題目】各項均為正數的數列{an}中,前n項和![]() .
.
(1)求數列{an}的通項公式;
(2)若![]() 恒成立,求k的取值范圍;
恒成立,求k的取值范圍;
(3)是否存在正整數m,k,使得am,am+5,ak成等比數列?若存在,求出m和k的值,若不存在,請說明理由.
【答案】(1)an=2n-1;(2)![]() ;(3)存在m=1,k=61滿足題意.
;(3)存在m=1,k=61滿足題意.
【解析】試題分析:
(1)由題中的遞推關系結合題意可得數列的通項公式為![]() ;
;
(2)首先裂項求數列的前n項和,然后結合恒成立的條件可得k的取值范圍是![]() ;
;
(3)由題中的結論討論可得存在m=1,k=61滿足題意.
試題解析:
(1)∵![]() ,∴
,∴![]() ,
,
兩式相減得![]() ,
,
整理得(an+an-1)(an-an-1-2)=0,
∵數列{an}的各項均為正數,∴an-an-1=2,n≥2,
∴{an}是公差為2的等差數列,
又![]() 得a1=1,∴an=2n-1.
得a1=1,∴an=2n-1.
(2)由題意得![]() ,
,
∵![]() ,
,
∴![]() =
=![]() ,
,
∴![]() .
.
(3)∵an=2n-1.
假設存在正整數m,k,使得am,am+5,ak成等比數列,即![]()
即(2m+9)2=(2m-1)(2k-1),
∵(2m-1)≠0,∴![]() ,
,
∵2k-1∈Z,∴2m-1為100的約數,
∴2m-1=1,m=1,k=61.


科目:高中數學 來源: 題型:
【題目】(數學(文)卷·2017屆湖北省沙市中學高三上學期第七次雙周練第16題)埃及數學中有一個獨特現象:除![]() 用一個單獨的符號表示以外,其它分數都要寫成若干個單分數和的形式.例如
用一個單獨的符號表示以外,其它分數都要寫成若干個單分數和的形式.例如![]() 可以這樣理解:假定有兩個面包,要平均分給5個人,如果每人
可以這樣理解:假定有兩個面包,要平均分給5個人,如果每人![]() ,不夠,每人
,不夠,每人![]() ,余
,余![]() ,再將這
,再將這![]() 分成5份,每人得
分成5份,每人得![]() ,這樣每人分得
,這樣每人分得![]() .形如
.形如![]() 的分數的分解:
的分數的分解: ![]() ,
, ![]() ,
, ![]() ,按此規律,
,按此規律, ![]() =____________;
=____________; ![]() = ____________
= ____________![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
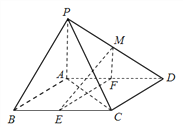
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形, ![]() ,側面
,側面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)如果直線![]() 與平面
與平面![]() 所成的角和直線
所成的角和直線![]() 與平面
與平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市理論預測2010年到2014年人口總數與年份的關系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口數y(十萬) | 5 | 7 | 8 | 11 | 19 |
(1)請根據上表提供的數據,求出y關于x的線性回歸方程;
(2) 據此估計2015年該城市人口總數。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在甲、乙兩個盒子中分別裝有標號為1,2,3,4的四個球,現從甲乙兩個盒子中各取出1個球,球的標號分別記做a,b,每個球被取出的可能性相等.
(1)求a+b能被3整除的概率;
(2)若|a-b|≤1則中獎,求中獎的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拖延癥總是表現在各種小事上,但日積月累,特別影響個人發展.某校的一個社會實踐調查小組,在對該校學生進行“是否有明顯拖延癥”的調查中,隨機發放了110份問卷.對收回的100份有效問卷進行統計,得到如下![]() 列聯表:
列聯表:
有明顯拖延癥 | 無明顯拖延癥 | 合計 | |
男 | 35 | 25 | 60 |
女 | 30 | 10 | 40 |
合計 | 65 | 35 | 100 |
(Ⅰ)按女生是否有明顯拖延癥進行分層,已經從40份女生問卷中抽取了8份問卷,現從這8份問卷中再隨機抽取3份,并記其中無明顯拖延癥的問卷的份數為![]() ,試求隨機變量
,試求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)若在犯錯誤的概率不超過![]() 的前提下認為無明顯拖延癥與性別有關,那么根據臨界值表,最精確的
的前提下認為無明顯拖延癥與性別有關,那么根據臨界值表,最精確的![]() 的值應為多少?請說明理由.
的值應為多少?請說明理由.
附:獨立性檢驗統計量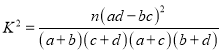 ,其中
,其中![]() .
.
獨立性檢驗臨界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
: ![]() 過橢圓
過橢圓![]() :
: ![]() (
(![]() )的短軸端點,
)的短軸端點, ![]() ,
, ![]() 分別是圓
分別是圓![]() 與橢圓
與橢圓![]() 上任意兩點,且線段
上任意兩點,且線段![]() 長度的最大值為3.
長度的最大值為3.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過點![]() 作圓
作圓![]() 的一條切線交橢圓
的一條切線交橢圓![]() 于
于![]() ,
, ![]() 兩點,求
兩點,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com