
【題目】已知復(fù)平面內(nèi)平行四邊形ABCD(A,B,C,D按逆時(shí)針排列),A點(diǎn)對(duì)應(yīng)的復(fù)數(shù)為2+i,向量![]() 對(duì)應(yīng)的復(fù)數(shù)為1+2i,向量
對(duì)應(yīng)的復(fù)數(shù)為1+2i,向量![]() 對(duì)應(yīng)的復(fù)數(shù)為3-i.
對(duì)應(yīng)的復(fù)數(shù)為3-i.
(1)求點(diǎn)C,D對(duì)應(yīng)的復(fù)數(shù).
(2)求平行四邊形ABCD的面積.
【答案】(1)4-2i 5
(2)7
【解析】
(1)設(shè)點(diǎn)O為原點(diǎn),因?yàn)橄蛄?/span>![]() 對(duì)應(yīng)的復(fù)數(shù)為1+2i,向量
對(duì)應(yīng)的復(fù)數(shù)為1+2i,向量![]() 對(duì)應(yīng)的復(fù)數(shù)為3-i,
對(duì)應(yīng)的復(fù)數(shù)為3-i,
所以向量![]() 對(duì)應(yīng)的復(fù)數(shù)為(3-i)-(1+2i)=2-3i,
對(duì)應(yīng)的復(fù)數(shù)為(3-i)-(1+2i)=2-3i,
又![]() =
=![]() +
+![]() ,
,
所以點(diǎn)C對(duì)應(yīng)的復(fù)數(shù)為(2+i)+(2-3i)=4-2i.
又![]() =
=![]() +
+![]() =(1+2i)+(3-i)=4+i,
=(1+2i)+(3-i)=4+i,
![]() =
=![]() -
-![]() =2+i-(1+2i)=1-i,
=2+i-(1+2i)=1-i,
所以![]() =
=![]() +
+![]() =1-i+(4+i)=5,
=1-i+(4+i)=5,
所以點(diǎn)D對(duì)應(yīng)的復(fù)數(shù)為5.
(2)由(1)知![]() =(1,2),
=(1,2),![]() =(3,-1),
=(3,-1),
因?yàn)?/span>![]() ·
·![]() =|
=|![]() ||
||![]() |cosB,
|cosB,
所以cosB=![]() =
=![]() =
=![]() ,
,
所以sinB=![]() ,
,
又|![]() |=
|=![]() ,|
,|![]() |=
|=![]() ,
,
所以面積S=|![]() ||
||![]() |sinB=
|sinB=![]() ×
×![]() ×
×![]() =7.
=7.
所以平行四邊形ABCD的面積為7.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校研究性學(xué)習(xí)小組發(fā)現(xiàn),學(xué)生上課的注意力指標(biāo)隨著聽課時(shí)間的變化而變化.老師講課開始時(shí)學(xué)生的興趣激增,接下來學(xué)生的興趣將保持較理想的狀態(tài)一段時(shí)間,隨后學(xué)生的注意力開始分散.該小組發(fā)現(xiàn)注意力指標(biāo)![]() 與上課時(shí)刻第
與上課時(shí)刻第![]() 分鐘末的關(guān)系如下(
分鐘末的關(guān)系如下(![]() ,設(shè)上課開始時(shí),t=0):
,設(shè)上課開始時(shí),t=0): .若上課后第5分鐘末時(shí)的注意力指標(biāo)為140.
.若上課后第5分鐘末時(shí)的注意力指標(biāo)為140.
(1)求![]() 的值;
的值;
(2)上課后第5分鐘末和第35分鐘末比較,哪個(gè)時(shí)刻注意力更集中?
(3)在一節(jié)課中,學(xué)生的注意力指標(biāo)至少達(dá)到140的時(shí)間能保持多長(zhǎng)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,A,B是圓O:
中,A,B是圓O:![]() 與x軸的兩個(gè)交點(diǎn)(點(diǎn)B在點(diǎn)A右側(cè)),點(diǎn)
與x軸的兩個(gè)交點(diǎn)(點(diǎn)B在點(diǎn)A右側(cè)),點(diǎn)![]() ,x軸上方的動(dòng)點(diǎn)P使直線
,x軸上方的動(dòng)點(diǎn)P使直線![]() ,
,![]() ,
,![]() 的斜率存在且依次成等差數(shù)列.
的斜率存在且依次成等差數(shù)列.

(1)求證:動(dòng)點(diǎn)P的橫坐標(biāo)為定值;
(2)設(shè)直線![]() ,
,![]() 與圓O的另一個(gè)交點(diǎn)分別為S,T.求證:點(diǎn)Q,S,T三點(diǎn)共線.
與圓O的另一個(gè)交點(diǎn)分別為S,T.求證:點(diǎn)Q,S,T三點(diǎn)共線.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 長(zhǎng)軸的兩個(gè)端點(diǎn)分別為
長(zhǎng)軸的兩個(gè)端點(diǎn)分別為![]() ,
,![]() , 離心率
, 離心率![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)作一條垂直于![]() 軸的直線,使之與橢圓
軸的直線,使之與橢圓![]() 在第一象限相交于點(diǎn)
在第一象限相交于點(diǎn)![]() ,在第四象限相交于點(diǎn)
,在第四象限相交于點(diǎn)![]() ,若直線
,若直線![]() 與直線
與直線![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,且直線
,且直線![]() 的斜率大于
的斜率大于![]() ,求直線
,求直線![]() 的斜率
的斜率![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知正三棱錐的高為6,側(cè)面與底面成![]() 的二面角,則其內(nèi)切球(與四個(gè)面都相切)的表面積為( )
的二面角,則其內(nèi)切球(與四個(gè)面都相切)的表面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在多面體![]() 中,
中,![]() 和
和![]() 交于一點(diǎn),除
交于一點(diǎn),除![]() 以外的其余各棱長(zhǎng)均為2.
以外的其余各棱長(zhǎng)均為2.
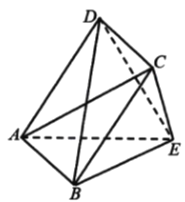
![]() 作平面
作平面![]() 與平面
與平面![]() 的交線
的交線![]() ,并寫出作法及理由;
,并寫出作法及理由;
![]() 求證:平面
求證:平面![]() 平面
平面![]() ;
;
![]() 若多面體的體積為2,求直線
若多面體的體積為2,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (其中
(其中![]() 為常數(shù)且
為常數(shù)且![]() )在
)在![]() 處取得極值.
處取得極值.
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 的極大值點(diǎn)和極小值點(diǎn);
的極大值點(diǎn)和極小值點(diǎn);
(2)若![]() 在
在![]() 上的最大值為1,求
上的最大值為1,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù) .
.
(1)求![]() 的零點(diǎn)之和;
的零點(diǎn)之和;
(2)已知![]() ,討論函數(shù)
,討論函數(shù)![]() 的零點(diǎn)個(gè)數(shù).
的零點(diǎn)個(gè)數(shù).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com