
已知二次函數 滿足以下兩個條件:
滿足以下兩個條件:
①不等式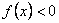 的解集是(-2,0) ②函數
的解集是(-2,0) ②函數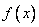 在
在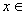
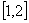 上的最小值是3
上的最小值是3
(Ⅰ)求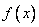 的解析式;
的解析式;
(Ⅱ)若點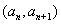
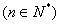 在函數
在函數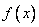 的圖象上,且
的圖象上,且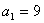
(ⅰ)求證:數列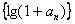 為等比數列
為等比數列
(ⅱ)令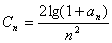 ,是否存在整數
,是否存在整數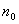 使得數列
使得數列 取到最小值?若有,請求出
取到最小值?若有,請求出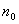 的值;沒有,請說明理由。
的值;沒有,請說明理由。
解:(Ⅰ)∵ f(x)< 0 的解集為(-2,0),且f(x)是二次函數
∴ 可設 f(x)= a x(x + 2) (a > 0),故 f(x)的對稱軸為直線 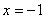 ,
,
∴ f(x)在 [1,2]上的最小值為f(1)=3a =3 ,
∴ a = 1 ,所以f(x)= x 2 + 2 x .
(Ⅱ)(ⅰ)∵ 點(a n , a n + 1 )在函數f(x)= x 2 + 2 x 的圖象上
∴ a n + 1 = a n 2 + 2 a n , 則 1 + a n + 1 = 1 + a n 2 + 2 a n = (1 + a n)2
∴ 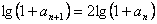 , 又首項
, 又首項 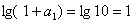
∴ 數列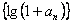 為等比數列,且公比為2 。
為等比數列,且公比為2 。
(ⅱ)由上題可知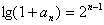 ,
,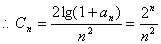 ,
,
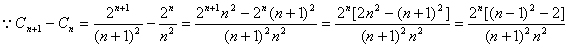
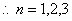 時,有
時,有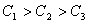 ,
,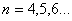 時,有
時,有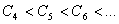
故只須比較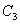 與
與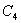 ,而
,而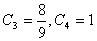 ,所以當
,所以當 時,數列
時,數列 取到最小值。
取到最小值。


科目:高中數學 來源: 題型:
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源:陜西省2009屆高三教學質量檢測模擬試題(一)、數學 題型:044
已知二次函數滿足以下條件:
①圖像關于直線x=![]() 對稱;②f(1)=0;③其圖像可由y=x2-1平移得到.
對稱;②f(1)=0;③其圖像可由y=x2-1平移得到.
(Ⅰ)求y=f(x)表達式;
(Ⅱ)若數列{an},{bn}對任意的實數x都滿足f(x)·g(x)+anx+bn=xn+1(n∈N*),其中g(x)是定義在實數集R上的一個函數,求數列{an},{bn}的通項公式.
(Ⅲ)設圓Cn:(x-an)2+(y-bn)2=![]() ,(n∈N*),若圓Cn與圓Cn+1外切,且{rn}是各項都為正數的等比數列,求數列{rn}的公比q的值.
,(n∈N*),若圓Cn與圓Cn+1外切,且{rn}是各項都為正數的等比數列,求數列{rn}的公比q的值.
查看答案和解析>>
科目:高中數學 來源:2014屆福建省高二上學期期中考試文科數學試卷(解析版) 題型:解答題
(本小題滿分14分)
已知二次函數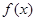 滿足以下兩個條件:
滿足以下兩個條件:
①不等式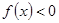 的解集是(-2,0) ②函數
的解集是(-2,0) ②函數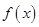 在
在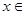
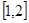 上的最小值是3
上的最小值是3
(Ⅰ)求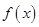 的解析式;
的解析式;
(Ⅱ)若點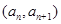
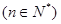 在函數
在函數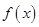 的圖象上,且
的圖象上,且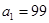
(ⅰ)求證:數列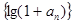 為等比數列
為等比數列
(ⅱ)令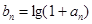 ,是否存在正實數
,是否存在正實數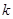 ,使不等式
,使不等式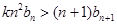 對于一切的
對于一切的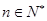 恒成立?若存在,指出
恒成立?若存在,指出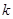 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com