
已知數(shù)列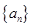 中,
中,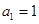 ,
, ,數(shù)列
,數(shù)列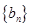 中,
中, ,且點(diǎn)
,且點(diǎn) 在直線(xiàn)
在直線(xiàn)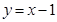 上.
上.
(Ⅰ)求數(shù)列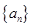 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅱ)求數(shù)列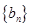 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅲ)若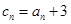 ,求數(shù)列
,求數(shù)列 的前項(xiàng)和
的前項(xiàng)和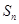 .
.
(Ⅰ) 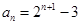 ;(Ⅱ)
;(Ⅱ)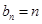 ;(Ⅲ)
;(Ⅲ)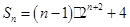 .
.
解析試題分析:(Ⅰ) 由已知可構(gòu)造數(shù)列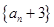 ,并證明其為等比數(shù)列,先求出數(shù)列
,并證明其為等比數(shù)列,先求出數(shù)列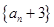 的通項(xiàng)公式,再求數(shù)列
的通項(xiàng)公式,再求數(shù)列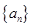 的通項(xiàng)公式(一般形如
的通項(xiàng)公式(一般形如 的遞推關(guān)系,可先構(gòu)造等比數(shù)列
的遞推關(guān)系,可先構(gòu)造等比數(shù)列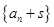 ,其公比
,其公比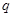 與常數(shù)
與常數(shù)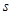 ,可由
,可由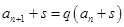 與所給等式
與所給等式 進(jìn)行比較求得);(Ⅱ)將點(diǎn)
進(jìn)行比較求得);(Ⅱ)將點(diǎn) 代入直線(xiàn)方程
代入直線(xiàn)方程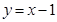 ,可得到數(shù)列
,可得到數(shù)列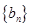 中
中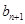 與
與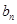 的關(guān)系式,從而發(fā)現(xiàn)
的關(guān)系式,從而發(fā)現(xiàn)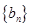 為等差數(shù)列,即可求出數(shù)列
為等差數(shù)列,即可求出數(shù)列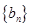 的通項(xiàng)公式;(Ⅲ)由(Ⅰ) (Ⅱ)可得數(shù)列
的通項(xiàng)公式;(Ⅲ)由(Ⅰ) (Ⅱ)可得數(shù)列 的通項(xiàng)公式,觀察
的通項(xiàng)公式,觀察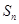 中各項(xiàng)關(guān)系,可用錯(cuò)位相減法來(lái)求出
中各項(xiàng)關(guān)系,可用錯(cuò)位相減法來(lái)求出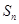 (錯(cuò)位相減法是求數(shù)列前項(xiàng)
(錯(cuò)位相減法是求數(shù)列前項(xiàng) 和的常用方法,它適用于如果一個(gè)數(shù)列的各項(xiàng)是由一個(gè)等差數(shù)列和一個(gè)等比數(shù)列的對(duì)應(yīng)各項(xiàng)之積構(gòu)成的).
和的常用方法,它適用于如果一個(gè)數(shù)列的各項(xiàng)是由一個(gè)等差數(shù)列和一個(gè)等比數(shù)列的對(duì)應(yīng)各項(xiàng)之積構(gòu)成的).
試題解析:(Ⅰ)由 得
得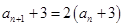
所以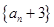 是首項(xiàng)為
是首項(xiàng)為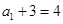 ,公比為2的等比數(shù)列.
,公比為2的等比數(shù)列.
所以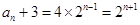 ,故
,故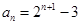
(Ⅱ)因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/26/f/ygpaf.png" style="vertical-align:middle;" />在直線(xiàn)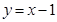 上,
上,
所以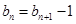 即
即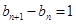 又
又
故數(shù)列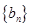 是首項(xiàng)為1,公差為1的等差數(shù)列,
是首項(xiàng)為1,公差為1的等差數(shù)列,
所以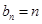
(Ⅲ)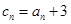 =
=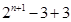 =
=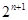 故
故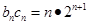
所以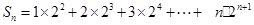
故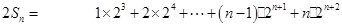
相減得
所以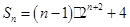
考點(diǎn):1.等比數(shù)列;2.等差數(shù)列;3.數(shù)列前項(xiàng) 和求法.
和求法.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知數(shù)列{an}是首項(xiàng)為-1,公差d  0的等差數(shù)列,且它的第2、3、6項(xiàng)依次構(gòu)成等比數(shù)列{bn}的前3項(xiàng)。
0的等差數(shù)列,且它的第2、3、6項(xiàng)依次構(gòu)成等比數(shù)列{bn}的前3項(xiàng)。
(1)求{an}的通項(xiàng)公式;
(2)若Cn=an·bn,求數(shù)列{Cn}的前n項(xiàng)和Sn。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
現(xiàn)在市面上有普通型汽車(chē)(以汽油為燃料)和電動(dòng)型汽車(chē)兩種。某品牌普通型汽車(chē)車(chē)價(jià)為12萬(wàn)元,第一年汽油的消費(fèi)為6000元,隨著汽油價(jià)格的不斷上升,汽油的消費(fèi)每年以20%的速度增長(zhǎng)。其它費(fèi)用(保險(xiǎn)及維修費(fèi)用等)第一年為5000元,以后每年遞增2000元。而電動(dòng)汽車(chē)由于節(jié)能環(huán)保,越來(lái)越受到社會(huì)認(rèn)可。某品牌電動(dòng)車(chē)在某市上市,車(chē)價(jià)為25萬(wàn)元,購(gòu)買(mǎi)時(shí)一次性享受?chē)?guó)家補(bǔ)貼價(jià)6萬(wàn)元和該市市政府補(bǔ)貼價(jià)4萬(wàn)元。電動(dòng)汽車(chē)動(dòng)力不靠燃油,而靠電池。電動(dòng)車(chē)使用的普通鋰電池平均使用壽命大約兩年(也即兩年需更換電池一次),電池價(jià)格為1萬(wàn)元,電動(dòng)汽車(chē)的其它費(fèi)用每年約為5000元。
求使用 年,普通型汽車(chē)的總耗資費(fèi)
年,普通型汽車(chē)的總耗資費(fèi)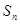 (萬(wàn)元)的表達(dá)式
(萬(wàn)元)的表達(dá)式
(總耗資費(fèi)=車(chē)價(jià)+汽油費(fèi)+其它費(fèi)用)
比較兩種汽車(chē)各使用10年的總耗資費(fèi)用
(參考數(shù)據(jù):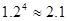
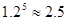
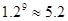
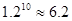 )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知各項(xiàng)都不相等的等差數(shù)列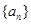 的前6項(xiàng)和為60,且
的前6項(xiàng)和為60,且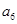 為
為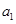 和
和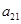 的等比中項(xiàng).
的等比中項(xiàng).
( I ) 求數(shù)列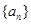 的通項(xiàng)公式;
的通項(xiàng)公式;
(II) 若數(shù)列 滿(mǎn)足
滿(mǎn)足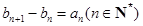 ,且
,且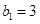 ,求數(shù)列
,求數(shù)列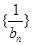 的前
的前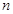 項(xiàng)和
項(xiàng)和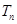 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知數(shù)列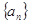 中,
中,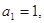 且點(diǎn)
且點(diǎn) 在直線(xiàn)
在直線(xiàn) 上。
上。
(1)求數(shù)列 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)若函數(shù)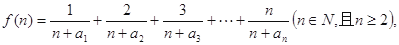 求函數(shù)
求函數(shù)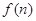 的最小值;
的最小值;
(3)設(shè) 表示數(shù)列
表示數(shù)列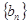 的前項(xiàng)和.試問(wèn):是否存在關(guān)于
的前項(xiàng)和.試問(wèn):是否存在關(guān)于 的整式
的整式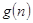 ,使得
,使得 對(duì)于一切不小于2的自然數(shù)
對(duì)于一切不小于2的自然數(shù) 恒成立?若存在,寫(xiě)出
恒成立?若存在,寫(xiě)出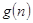 的解析式,并加以證明;若不存在,試說(shuō)明理由。
的解析式,并加以證明;若不存在,試說(shuō)明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
在等比數(shù)列{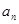 }中,
}中, ,公比
,公比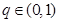 ,且
,且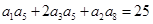 ,
,  與
與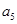 的等比中項(xiàng)為2.
的等比中項(xiàng)為2.
(1)求數(shù)列{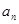 }的通項(xiàng)公式;
}的通項(xiàng)公式;
(2)設(shè)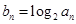 ,求:數(shù)列{
,求:數(shù)列{ }的前
}的前 項(xiàng)和為
項(xiàng)和為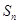 ,
,
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知數(shù)列{an}滿(mǎn)足: ,
, ,
,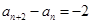
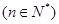
(Ⅰ)求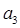

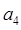 ,并求數(shù)列{an}通項(xiàng)公式;
,并求數(shù)列{an}通項(xiàng)公式;
(Ⅱ)記數(shù)列{an}前2n項(xiàng)和為 ,當(dāng)
,當(dāng) 取最大值時(shí),求
取最大值時(shí),求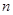 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知等差數(shù)列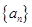 的公差
的公差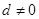 ,它的前
,它的前 項(xiàng)和為
項(xiàng)和為 ,若
,若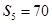 ,且
,且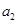 、
、 、
、 成等比數(shù)列.
成等比數(shù)列.
(1)求數(shù)列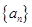 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)設(shè)數(shù)列 的前
的前 項(xiàng)和為
項(xiàng)和為 ,求證:
,求證: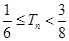 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知等差數(shù)列 滿(mǎn)足:
滿(mǎn)足: ,
, 的前n項(xiàng)和為
的前n項(xiàng)和為 .
.
(1)求 及
及 ;
;
(2)已知數(shù)列 的第n項(xiàng)為
的第n項(xiàng)為 ,若
,若 成等差數(shù)列,且
成等差數(shù)列,且 ,設(shè)數(shù)列
,設(shè)數(shù)列 的前
的前 項(xiàng)和
項(xiàng)和 .求數(shù)列
.求數(shù)列 的前
的前 項(xiàng)和
項(xiàng)和 .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com