
在一條筆直的工藝流水線上有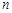 個工作臺,將工藝流水線用如圖
個工作臺,將工藝流水線用如圖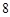 所示的數軸表示,各工作臺的坐標分別為
所示的數軸表示,各工作臺的坐標分別為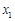 ,
,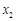 ,
,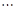 ,
,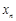 ,每個工作臺上有若干名工人.現要在流水線上建一個零件供應站,使得各工作臺上的所有工人到供應站的距離之和最短.
,每個工作臺上有若干名工人.現要在流水線上建一個零件供應站,使得各工作臺上的所有工人到供應站的距離之和最短.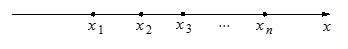
(Ⅰ)若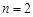 ,每個工作臺上只有一名工人,試確定供應站的位置;
,每個工作臺上只有一名工人,試確定供應站的位置;
(Ⅱ)若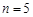 ,工作臺從左到右的人數依次為
,工作臺從左到右的人數依次為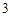 ,
,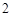 ,
,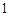 ,
,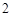 ,
,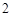 ,試確定供應站的位置,并求所有工人到供應站的距離之和的最小值.
,試確定供應站的位置,并求所有工人到供應站的距離之和的最小值.
(Ⅰ)設供應站坐標為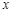 ,根據兩點間距離最短,列出各工作臺上的所有工人到供應站的距離之和為
,根據兩點間距離最短,列出各工作臺上的所有工人到供應站的距離之和為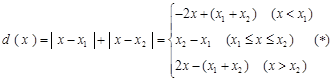 ,然后分段討論,去掉絕對值符號,化為分段函數,求函數
,然后分段討論,去掉絕對值符號,化為分段函數,求函數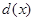 取最小值滿足的條件即可.(Ⅱ)同(Ⅰ)首先列出各工作臺上的所有工人到供應站的距離之和為
取最小值滿足的條件即可.(Ⅱ)同(Ⅰ)首先列出各工作臺上的所有工人到供應站的距離之和為 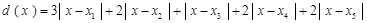 ,然后分段討論,去掉絕對值符號,化為分段函數,求函數
,然后分段討論,去掉絕對值符號,化為分段函數,求函數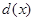 取最小值滿足的條件即可.
取最小值滿足的條件即可.
解析試題分析:設供應站坐標為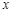 ,各工作臺上的所有工人到供應站的距離之和為
,各工作臺上的所有工人到供應站的距離之和為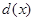 .
.
(Ⅰ)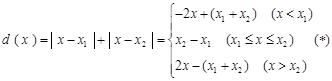 2分
2分
當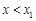 時,
時,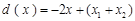 在區間
在區間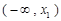 上是減函數;
上是減函數;
當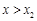 時,
時,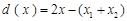 在區間
在區間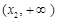 上是增函數.
上是增函數.
則當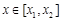 時,
時,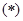 式取最小值,即供應站的位置為
式取最小值,即供應站的位置為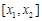 內的任意一點.
內的任意一點. 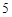 分
分
(Ⅱ)由題設知,各工作臺上的所有工人到供應站的距離之和為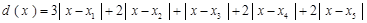 . 7分
. 7分
類似于(Ⅰ)的討論知,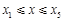 ,且有
,且有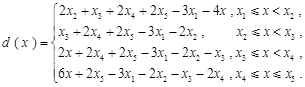
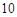 分
分
所以,函數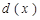 在區間
在區間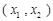 上是減函數,在區間
上是減函數,在區間 上是增函數,在區間
上是增函數,在區間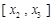 上是常數.故供應站位置位于區間
上是常數.故供應站位置位于區間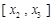 上任意一點時,均能使函數
上任意一點時,均能使函數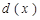 取得最小值,且最小值為
取得最小值,且最小值為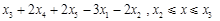 . 13分
. 13分
考點:綜合運用函數知識解決實際問題的能力


科目:高中數學 來源: 題型:解答題
心理學家通過研究學生的學習行為發現;學生的接受能力與老師引入概念和描述問題所用的時間相關,教學開始時,學生的興趣激增,學生的興趣保持一段較理想的狀態,隨后學生的注意力開始分散,分析結果和實驗表明,用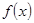 表示學生掌握和接受概念的能力, x表示講授概念的時間(單位:min),可有以下的關系:
表示學生掌握和接受概念的能力, x表示講授概念的時間(單位:min),可有以下的關系: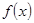
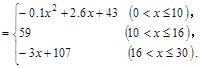
(1)開講后第5min與開講后第20min比較,學生的接受能力何時更強一些?
(2)開講后多少min學生的接受能力最強?能維持多少時間?
(3)若一個新數學概念需要55以上(包括55)的接受能力以及13min時間,那么老師能否在學生一直達到所需接受能力的狀態下講授完這個概念?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對定義在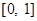 上,并且同時滿足以下兩個條件的函數
上,并且同時滿足以下兩個條件的函數 稱為
稱為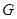 函數。
函數。
①對任意的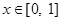 ,總有
,總有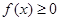 ;
;
②當 時,總有
時,總有 成立。
成立。
已知函數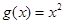 與
與 是定義在
是定義在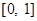 上的函數。
上的函數。
(1)試問函數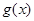 是否為
是否為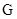 函數?并說明理由;
函數?并說明理由;
(2)若函數 是
是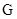 函數,求實數
函數,求實數 的值;
的值;
(3)在(2)的條件下,討論方程
 解的個數情況。
解的個數情況。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠某種產品的年固定成本為250萬元,每生產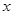 千件,需另投入成本為
千件,需另投入成本為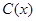 ,當年產量不足80千件時,
,當年產量不足80千件時,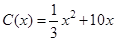 (萬元).當年產量不小于80千件時,
(萬元).當年產量不小于80千件時, (萬元).每件商品售價為500元.通過市場分析,該廠生產的商品能全部售完.
(萬元).每件商品售價為500元.通過市場分析,該廠生產的商品能全部售完.
(1)寫出年利潤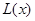 (萬元)關于年產量
(萬元)關于年產量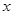 (千件)的函數解析式;
(千件)的函數解析式;
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某廠生產某種產品的年固定成本為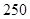 萬元,每生產
萬元,每生產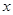 千件,需另投入成本為
千件,需另投入成本為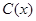 .當年產量不足
.當年產量不足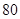 千件時,
千件時,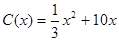 (萬元).當年產量不小于
(萬元).當年產量不小于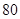 千件時,
千件時,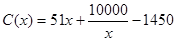 (萬元).每件商品售價為
(萬元).每件商品售價為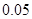 萬元.通過市場分析,該廠生產的商品能全部售完.
萬元.通過市場分析,該廠生產的商品能全部售完.
(1)寫出年利潤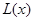 (萬元)關于年產量
(萬元)關于年產量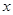 (千件)的函數解析式;
(千件)的函數解析式;
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com