亚洲最新免费视频,国产一区香蕉久久,国产美女直播视频一区

【題目】某二手車交易市場對某型號的二手汽車的使用年數與銷售價格（單位：萬元/輛）進行整理，得到如下的對應數據：

使用年數	2	4	6	8	10
售價	16	13	9.5	7	4.5

（1）試求關于的回歸直線方程：（參考公式：, ．）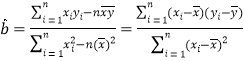

（2）已知每輛該型號汽車的收購價格為萬元，根據（1）中所求的回歸方程，預測為何值時，銷售一輛該型號汽車所獲得的利潤最大？

【答案】（1）；（2）.

【解析】分析：（1）利用表中數據求出回歸直線方程，（2）寫出利潤函數,利用二次函數的圖像與性質求出x=3時z的最大值。

詳解：（1）由已知：，

則，

所以回歸直線的方程為．

（2）z=﹣1.45x+18.7﹣（0.05x2﹣1.75x+17.2）

=﹣0.052x2+0.3x+1.5

=﹣0.05（x﹣3）2+1.95，

所以預測當x=3時，銷售利潤z取得最大值．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】正方形和四邊形所在的平面互相垂直，，，.

求證：(1) 平面；

(2) 平面.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖，四棱錐P﹣ABCD，底面是以O為中心的菱形，PO⊥底面ABCD，AB=2，∠BAD= ，M為BC上的一點，且BM= ，MP⊥AP．

（1）求PO的長；
（2）求二面角A﹣PM﹣C的正弦值．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】記max{x，y}= ，min{x，y}= ，設，為平面向量，則（）
A.min{| + |，| ﹣ |}≤min{| |，| |}
B.min{| + |，| ﹣ |}≥min{| |，| |}
C.max{| + |2 ， | ﹣ |2}≤| |2+| |2
D.max{| + |2 ， | ﹣ |2}≥| |2+| |2

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】設數列{an}的前n項和為Sn．已知S2=4,an+1=2Sn+1,n∈N*．

(1)求通項公式an;

(2)求數列{|an-n-2|}的前n項和．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖，在四棱錐A﹣BCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED=90°，AB=CD=2，DE=BE=1，AC= ．

（1）證明：DE⊥平面ACD；
（2）求二面角B﹣AD﹣E的大小．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】九章算術是我國古代著名數學經典其中對勾股定理的論述比西方早一千多年，其中有這樣一個問題：“今有圓材埋在壁中，不知大小以鋸鋸之，深一寸，鋸道長一尺問徑幾何？”其意為：今有一圓柱形木材，埋在墻壁中，不知其大小，用鋸去鋸該材料，鋸口深一寸，鋸道長一尺問這塊圓柱形木料的直徑是多少？長為1丈的圓柱形木材部分鑲嵌在墻體中，截面圖如圖所示陰影部分為鑲嵌在墻體內的部分已知弦尺，弓形高寸，估算該木材鑲嵌在墻中的體積約為( )(注：1丈尺寸，，)