【題目】已知圓
，圓
內一定點
，動圓
過點
且與圓內切.記動圓圓心的軌跡為
.
（Ⅰ）求軌跡方程；
（II）過點
的動直線l交軌跡于M，N兩點，試問：在坐標平面上是否存在一個定點Q，使得以線段MN為直徑的圓恒過點Q？若存在，求出點Q的坐標；若不存在，請說明理由.
【答案】(I) 
；(II)存在，恒過點Q(0，1).
【解析】
（Ⅰ）由題意可知：
，P點軌跡是以A、B為焦點的橢圓，即可求得橢圓的標準方程；
（Ⅱ）利用特例先確定定點Q，再推廣到一般情況即可.
解:（Ⅰ）解：設動圓圓心
，半徑為
.
，
故點
的軌跡為橢圓，
，
，
故圓心的軌跡方程為
(II)當l與x軸平行時，以線段MN為直徑的圓的方程為x2＋
＝
；
當l與y軸平行時，以線段MN為直徑的圓的方程為x2＋y2＝1.
由
得
故若存在定點Q，則Q的坐標只可能為Q(0，1).
下面證明Q(0，1)為所求：
若直線l的斜率不存在，上述已經證明.
若直線l的斜率存在，設直線l：y＝kx－
，
M(x1，y1)，N(x2，y2)，
由
得(9＋18k2)x2－12kx－16＝0，
Δ＝144k2＋64(9＋18k2)＞0，
x1＋x2＝
，x1x2＝
，
＝(x1，y1－1)，
＝(x2，y2－1)，
＝x1x2＋(y1－1)(y2－1)
＝(1＋k2)x1x2－
(x1＋x2)＋
＝(1＋k2)·
－·
＋＝0，
∴⊥，即以線段MN為直徑的圓恒過點Q(0，1).
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，直線
的參數方程為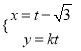
（
為參數），直線
的參數程為
（
為參數），設直線
與
的交點為
,當
變化時點
的軌跡為曲線
.
（1）求出曲線
的普通方程；
（2）以坐標原點為極點， 
軸的正半軸為極軸建立極坐標系，直線
的極坐標方程為
，點
為曲線
的動點，求點
到直線
的距離的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2017年是某市大力推進居民生活垃圾分類的關鍵一年，有關部門為宣傳垃圾分類知識，面向該市市民進行了一次“垃圾分類知識”的網絡問卷調查，每位市民僅有一次參與機會，通過抽樣，得到參與問卷調查中的1000人的得分數據，其頻率分布直方圖如圖所示：
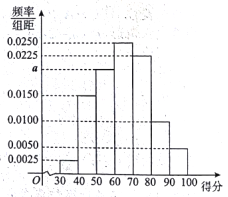
(Ⅰ)估計該組數據的中位數、眾數；
(Ⅱ)由頻率分布直方圖可以認為，此次問卷調查的得分Z服從正態分布N(μ，210)，μ近似為這1000人得分的平均值(同一組數據用該區間的中點值作代表)，利用該正態分布，求P(50.5<Z<94)；
(Ⅲ)在(Ⅱ)的條件下，有關部門為此次參加問卷調査的市民制定如下獎勵方案：
(i)得分不低于μ可獲贈2次隨機話費，得分低于μ則只有1次；
(ii)每次贈送的隨機話費和對應概率如下：
贈送話費(單元：元) | 10 | 20 |
概率 |
|
|
現有一位市民要參加此次問卷調查，記X(單位：元)為該市民參加.問卷調查獲贈的話費，求X的分布列和數學期望.
附： 
，
若ZN(μ，σ2)，則P(μ－σ<Z<μ+σ)= 0.6826，P(μ－2σ<Z<μ+2σ)=0.9544.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】兩人約定在20∶00到21∶00之間相見，并且先到者必須等遲到者40分鐘方可離去，如果兩人出發是各自獨立的，在20∶00至21∶00各時刻相見的可能性是相等的，則他們兩人在約定時間內相見的概率為（ ）．
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線C：
，點
在x軸的正半軸上，過點M的直線l與拋線C相交于A、B兩點，O為坐標原點．
若
，且直線l的斜率為1，求證：以AB為直徑的圓與拋物線C的準線相切；
是否存在定點M，使得不論直線l繞點M如何轉動，
恒為定值？若存在，請求出點M的坐標；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
