
【題目】下面有命題: ①y=|sinx﹣ ![]() |的周期是π;
|的周期是π;
②y=sinx+sin|x|的值域是[0,2];
③方程cosx=lgx有三解;
④ω為正實(shí)數(shù),y=2sinωx在 ![]() 上遞增,那么ω的取值范圍是
上遞增,那么ω的取值范圍是 ![]() ;
;
⑤在y=3sin(2x+ ![]() )中,若f(x1)=f(x2)=0,則x1﹣x2必為π的整數(shù)倍;
)中,若f(x1)=f(x2)=0,則x1﹣x2必為π的整數(shù)倍;
⑥若A、B是銳角△ABC的兩個(gè)內(nèi)角,則點(diǎn)P(cosB﹣sinA,sinB﹣cosA在第二象限;
⑦在△ABC中,若 ![]() ,則△ABC鈍角三角形.其中真命題個(gè)數(shù)為( )
,則△ABC鈍角三角形.其中真命題個(gè)數(shù)為( )
A.2
B.3
C.4
D.5
【答案】C
【解析】解:對(duì)于①,∵y=|sin(ωx﹣ ![]() |的周期是
|的周期是 ![]() ,故正確; 對(duì)于②,當(dāng)x≥0時(shí),y=sinx+sin|x|=2sinx值域不是[0,2],故錯(cuò);
,故正確; 對(duì)于②,當(dāng)x≥0時(shí),y=sinx+sin|x|=2sinx值域不是[0,2],故錯(cuò);
對(duì)于③,∵lg2π<1,lg4π>1,方程cosx=lgx有三解,正確;
對(duì)于④,ω為正實(shí)數(shù),y=2sinωx在 ![]() 上遞增,由條件利用正弦函數(shù)的單調(diào)性可得ω
上遞增,由條件利用正弦函數(shù)的單調(diào)性可得ω ![]() ≤,由此求得正數(shù)ω的范圍是
≤,由此求得正數(shù)ω的范圍是 ![]() ,故正確;
,故正確;
對(duì)于⑤,函數(shù)的周期T=π,函數(shù)值等于0的x之差的最小值為 ![]() ,所以x1﹣x2必是
,所以x1﹣x2必是 ![]() 的整數(shù)倍.故錯(cuò);
的整數(shù)倍.故錯(cuò);
對(duì)于⑥,若A、B是銳角△ABC的兩個(gè)內(nèi)角, ![]() B>
B> ![]() ﹣A,則 cosB﹣sinA<0,sinB﹣cosA>0,故正確;
﹣A,則 cosB﹣sinA<0,sinB﹣cosA>0,故正確;
故選:C.
【考點(diǎn)精析】本題主要考查了命題的真假判斷與應(yīng)用的相關(guān)知識(shí)點(diǎn),需要掌握兩個(gè)命題互為逆否命題,它們有相同的真假性;兩個(gè)命題為互逆命題或互否命題,它們的真假性沒(méi)有關(guān)系才能正確解答此題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】甲、乙兩名選手參加歌手大賽時(shí),5名評(píng)委打的分?jǐn)?shù)用莖葉圖表示(如圖).s1、s2分別表示甲、乙選手分?jǐn)?shù)的標(biāo)準(zhǔn)差,則s1與s2的關(guān)系是( ) 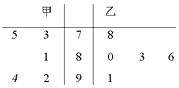
A.s1>s2
B.s1=s2
C.s1<s2
D.不確定
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】我們稱滿足: ![]() (
(![]() )的數(shù)列
)的數(shù)列![]() 為“
為“![]() 級(jí)夢(mèng)數(shù)列”.
級(jí)夢(mèng)數(shù)列”.
(1)若![]() 是“
是“![]() 級(jí)夢(mèng)數(shù)列”且
級(jí)夢(mèng)數(shù)列”且![]() .求:
.求: ![]() 和
和![]() 的值;
的值;
(2)若![]() 是“
是“![]() 級(jí)夢(mèng)數(shù)列”且滿足
級(jí)夢(mèng)數(shù)列”且滿足![]() ,
, ![]() ,求
,求![]() 的最小值;
的最小值;
(3)若![]() 是“0級(jí)夢(mèng)數(shù)列”且
是“0級(jí)夢(mèng)數(shù)列”且![]() ,設(shè)數(shù)列
,設(shè)數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() .證明:
.證明: ![]() (
(![]() ).
).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某同學(xué)用“五點(diǎn)法”畫(huà)函數(shù) ![]() 在區(qū)間[﹣
在區(qū)間[﹣ ![]() ,
, ![]() ]上的圖象時(shí),列表并填入了部分?jǐn)?shù)據(jù),如表:
]上的圖象時(shí),列表并填入了部分?jǐn)?shù)據(jù),如表:
2x﹣ | ﹣ | ﹣π | ﹣ | 0 |
|
|
x | ﹣ | ﹣ | ﹣ |
|
|
|
f(x) |
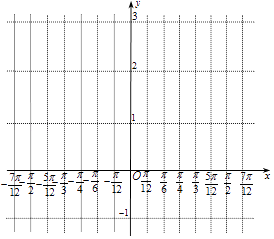
(1)請(qǐng)將上表數(shù)據(jù)補(bǔ)充完整,并在給出的直角坐標(biāo)系中,畫(huà)出f(x)在區(qū)間[﹣ ![]() ,
, ![]() ]上的圖象;
]上的圖象;
(2)求f(x)的最小值及取最小值時(shí)x的集合;
(3)求f(x)在 ![]() 時(shí)的值域.
時(shí)的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,有一塊半圓形空地,開(kāi)發(fā)商計(jì)劃建一個(gè)矩形游泳池![]() 及其矩形附屬設(shè)施
及其矩形附屬設(shè)施![]() ,并將剩余空地進(jìn)行綠化,園林局要求綠化面積應(yīng)最大化.其中半圓的圓心為
,并將剩余空地進(jìn)行綠化,園林局要求綠化面積應(yīng)最大化.其中半圓的圓心為![]() ,半徑為
,半徑為![]() ,矩形的一邊
,矩形的一邊![]() 在直徑上,點(diǎn)
在直徑上,點(diǎn)![]() 、
、![]() 、
、![]() 、
、![]() 在圓周上,
在圓周上,![]() 、
、![]() 在邊
在邊![]() 上,且
上,且![]() ,設(shè)
,設(shè)![]() .
.
(1)記游泳池及其附屬設(shè)施的占地面積為![]() ,求
,求![]() 的表達(dá)式;
的表達(dá)式;
(2)怎樣設(shè)計(jì)才能符合園林局的要求?

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知集合A={x|1<x<3},集合B={x|2m<x<1﹣m}.
(1)若m=﹣1求A∩B;
(2)若A∩B=,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,以橢圓長(zhǎng)、短軸四個(gè)端點(diǎn)為頂點(diǎn)為四邊形的面積為
,以橢圓長(zhǎng)、短軸四個(gè)端點(diǎn)為頂點(diǎn)為四邊形的面積為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
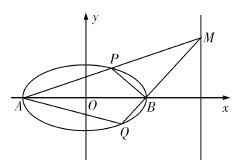
(Ⅱ)如圖所示,記橢圓的左、右頂點(diǎn)分別為![]() 、
、![]() ,當(dāng)動(dòng)點(diǎn)
,當(dāng)動(dòng)點(diǎn)![]() 在定直線
在定直線![]() 上運(yùn)動(dòng)時(shí),直線
上運(yùn)動(dòng)時(shí),直線![]() 分別交橢圓于兩點(diǎn)
分別交橢圓于兩點(diǎn)![]() 、
、![]() ,求四邊形
,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某體育場(chǎng)要建造一個(gè)長(zhǎng)方形游泳池,其容積為4800m3 , 深為3m,如果建造池壁的單價(jià)為a且建造池底的單價(jià)是建造池壁的1.5倍,怎樣設(shè)計(jì)水池的長(zhǎng)和寬,才能使總造價(jià)最底?最低造價(jià)是多少?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com