Question

【題目】已知數列{an}共有2k項（），數列{an}的前n項和為Sn，滿足：a1 = 2，an1 = (p 1) Sn 2（n = 1，2，…， 2k1），其中常數p > 1．

（1）求證：數列{an}是等比數列；

（2）若，數列{bn }滿足（n = 1，2，…， 2k），求數列

{bn }的通項公式；

（3）對于（2）中數列{bn }，求和Tn = ．

Answer 1

【答案】（1）見解析（2）（3）

【解析】試題分析：（1）先根據關系 得遞推關系式： ，再根據等比數列定義得證（2）先根據等比數列通項公式得an = a1p n 1．代入條件，利用指數性質化簡得 ．（3）關鍵取絕對值，因為，所以當n≤k時， ；當n≥k1時， ．再分別按等差數列求和得結果.

試題解析：解：（1）∵an1 = (p 1)Sn 2（n = 1，2，…， 2k1），

∴an = (p 1)Sn 1 2（n = 2，…， 2k）．

則當n = 2，…， 2k1時，兩式相減，得

an1 an = (p 1)（Sn Sn 1），即an1 an = (p 1) an．

∴an1 = pan（n = 2，…， 2k1）．

原式中，令n = 1，得a2 = (p 1)a1 2 = 2 (p 1) 2 = 2p = pa1．

∴an1 = pan，即（n = 1，2，…， 2k1）．

則數列{an}是等比數列．

（2）由（1），得an = a1p n 1．

∴

．

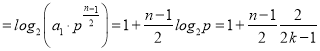
（3）∵，

∴當n≤k時， ；當n≥k1時， ．

則Tn =

=

= =

=．