
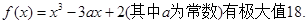
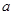 的值;
的值;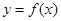 過原點的切線與函數
過原點的切線與函數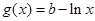 的圖像有兩個交點,試求b的取值范圍.
的圖像有兩個交點,試求b的取值范圍.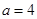 ;(Ⅱ)
;(Ⅱ)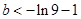 。
。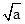 ,討論函數的單調性,進而求解函數的極值,從而可求a
,討論函數的單調性,進而求解函數的極值,從而可求a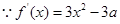 ,又函數
,又函數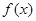 有極大值
有極大值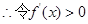 ,得
,得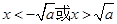
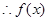 在
在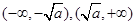 上遞增,在
上遞增,在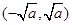 上遞減
上遞減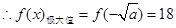 ,得
,得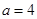 …………………………7分
…………………………7分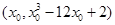 ,則切線斜率
,則切線斜率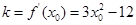
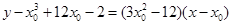
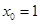 ,所以
,所以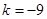
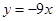
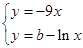 得
得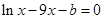
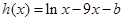
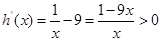 ,得
,得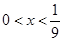
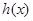 在
在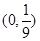 上遞增,在
上遞增,在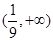 上遞減
上遞減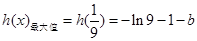
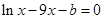 有兩個解,則
有兩個解,則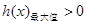
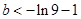 …………………………15分
…………………………15分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com