
【題目】設數列 ![]() 的前n項和為Sn
的前n項和為Sn ![]() ,且滿足:
,且滿足:
① ![]() ;②
;② ![]() ,其中
,其中 ![]() 且
且 ![]() .
.
(1)求p的值;
(2)數列 ![]() 能否是等比數列?請說明理由;
能否是等比數列?請說明理由;
(3)求證:當r ![]() 2時,數列
2時,數列 ![]() 是等差數列.
是等差數列.
【答案】
(1)
解:(1)n ![]() 1時,
1時, ![]() ,
,
因為 ![]() ,所以
,所以 ![]() ,
,
又 ![]() ,所以p
,所以p ![]() 1.
1.
(2)![]()
不是等比數列.理由如下:
假設 ![]() 是等比數列,公比為q,
是等比數列,公比為q,
當n ![]() 2時,
2時, ![]() ,即
,即 ![]() ,
,
所以 ![]() (i)
(i)
當n ![]() 3時,
3時, ![]() ,即
,即 ![]() ,
,
所以 ![]() , (ii)
, (ii)
由(i)(ii)得q ![]() 1,與
1,與 ![]() 矛盾,所以假設不成立.
矛盾,所以假設不成立.
故 ![]() 不是等比數列.
不是等比數列.
(3)
當r ![]() 2時,易知
2時,易知 ![]() .
.
由 ![]() ,得
,得
![]() 時,
時, ![]() , ①
, ①
![]() ,②
,②
②-①得, ![]() ,
,
即 ![]() ,
,
![]() ,
,
即 ![]()
![]()
![]() ……
……
![]() ,
,
所以 ![]()
令 ![]() d,則
d,則 ![]()
![]() .
.
所以 ![]() .
.
又 ![]() 時,也適合上式,
時,也適合上式,
所以 ![]() .
.
所以 ![]() .
.
所以當r ![]() 2時,數列
2時,數列 ![]() 是等差數列.
是等差數列.
【解析】(1.)將n=1代入②得 ![]() 分析可知只能是
分析可知只能是 ![]() =0,可算出p
=0,可算出p
(2.)假設是等比數列,將n=2、3分別代入得到q,判斷是否與已知條件矛盾.
(3.)當n=2時,用前 ![]() 項和減去
項和減去 ![]() 項和可得
項和可得 ![]() 之間關系,分析判斷可證
之間關系,分析判斷可證 ![]() 是等差數列.
是等差數列.
【考點精析】利用數列的通項公式對題目進行判斷即可得到答案,需要熟知如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】在四棱錐P﹣ABCD中,PA⊥底面ABCD,底面ABCD為正方形,PA=AB,該四棱錐被一平面截去一部分后,剩余部分的三視圖如圖,則剩余部分體積與原四棱錐體積的比值為( )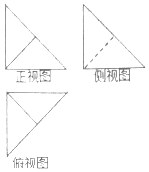
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A.若p:?x∈R,x2﹣x+1≥0,則¬p:?x∈R,x2﹣x+1<0
B.“ ![]() ”是“θ=30°或θ=150°”的充分不必要條件
”是“θ=30°或θ=150°”的充分不必要條件
C.命題“若a=0,則ab=0”的否命題是“若a≠0,則ab≠0”
D.已知p:?x∈R,cosx=1,q:?x∈R,x2﹣x+2>0,則“p∧(¬q)”為假命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐S﹣ABCD中,AB∥CD,BC⊥CD,側面SAB為等邊三角形,AB=BC=2,CD=SD=1.
(Ⅰ)證明:SD⊥平面SAB;
(Ⅱ)求AB與平面SBC所成的角的大小.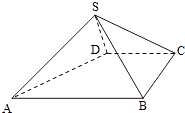
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)的圖象在點(x0 , f(x0))處的切線方程l:y=g(x),若函數f(x)滿足x∈I(其中I為函數f(x)的定義域),當x≠x0時,[f(x)﹣g(x)](x﹣x0)>0恒成立,則稱x0為函數f(x)的“穿越點”.已知函數f(x)=lnx﹣ ![]() x2﹣
x2﹣ ![]() 在(0,e]上存在一個“穿越點”,則a的取值范圍為( )
在(0,e]上存在一個“穿越點”,則a的取值范圍為( )
A.[ ![]() ,+∞)??
,+∞)??
B.(﹣1, ![]() ]??
]??
C.[﹣ ![]() ,1)??
,1)??
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=e1﹣x(﹣a+cosx),a∈R.
(Ⅰ)若函數y=f(x)在[0,π]存在單調增區間,求實數a的取值范圍;
(Ⅱ)若f( ![]() )=0,證明:對于x∈[﹣1,
)=0,證明:對于x∈[﹣1, ![]() ],總有f(﹣x﹣1)+2f′(x)cos(﹣x﹣1)>0.
],總有f(﹣x﹣1)+2f′(x)cos(﹣x﹣1)>0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直三棱柱ABC﹣A1B1C1中,AA1=AB=AC=1,E,F分別是CC1 , BC的中點,AE⊥A1B1 , D為棱A1B1上的點. 
(1)證明:AB⊥AC;
(2)證明:DF⊥AE;
(3)是否存在一點D,使得平面DEF與平面ABC所成銳二面角的余弦值為 ![]() ?若存在,說明點D的位置,若不存在,說明理由.
?若存在,說明點D的位置,若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com