
已知數列{ }中,
}中, 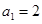 ,
,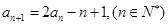 ,
,
(1)求證數列{
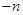 }為等比數列.
}為等比數列.
(2)判斷265是否是數列{ }中的項,若是,指出是第幾項,并求出該項以前所有項的和(不含265),若不是,說明理由.
}中的項,若是,指出是第幾項,并求出該項以前所有項的和(不含265),若不是,說明理由.
 智慧小復習系列答案
智慧小復習系列答案科目:高中數學 來源: 題型:解答題
已知數列{an}的前n項和為Sn,a1=2.當n≥2時,Sn-1+1,an,Sn+1成等差數列.
(1)求證:{Sn+1}是等比數列;
(2)求數列{nan}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(12分)(2011•重慶)設實數數列{an}的前n項和Sn滿足Sn+1=an+1Sn(n∈N*).
(Ⅰ)若a1,S2,﹣2a2成等比數列,求S2和a3.
(Ⅱ)求證:對k≥3有0≤ak≤ .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某市為控制大氣PM2.5的濃度,環境部門規定:該市每年的大氣主要污染物排放總量不能超過55萬噸,否則將采取緊急限排措施.已知該市2013年的大氣主要污染物排放總量為40萬噸,通過技術改造和倡導綠色低碳生活等措施,此后每年的原大氣主要污染物排放最比上一年的排放總量減少10%.同時,因為經濟發展和人口增加等因素,每年又新增加大氣主要污染物排放量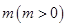 萬噸.
萬噸.
(1)從2014年起,該市每年大氣主要污染物排放總量(萬噸)依次構成數列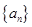 ,求相鄰兩年主要污染物排放總量的關系式;
,求相鄰兩年主要污染物排放總量的關系式;
(2)證明:數列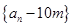 是等比數列;
是等比數列;
(3)若該市始終不需要采取緊急限排措施,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2013•湖北)已知等比數列{an}滿足:|a2﹣a3|=10,a1a2a3=125.
(1)求數列{an}的通項公式;
(2)是否存在正整數m,使得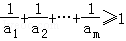 ?若存在,求m的最小值;若不存在,說明理由.
?若存在,求m的最小值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
學校餐廳每天供應500名學生用餐,每星期一有A, B兩種菜可供選擇。調查表明,凡是在這星期一選A菜的,下星期一會有 改選B菜;而選B菜的,下星期一會有
改選B菜;而選B菜的,下星期一會有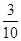 改選A菜。用
改選A菜。用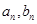 分別表示第
分別表示第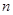 個星期選A的人數和選B的人數.
個星期選A的人數和選B的人數.
⑴試用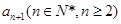 表示
表示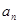 ,判斷數列
,判斷數列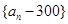 是否成等比數列并說明理由;
是否成等比數列并說明理由;
⑵若第一個星期一選A種菜的有200人,那么第10個星期一選A種菜的大約有多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在等比數列{an}中,a2a3=32,a5=32.
(1)求數列{an}的通項公式;
(2)設數列{an}的前n項和為Sn,求S1+2S2+…+nSn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com