
【題目】已知極坐標系的極點與直角坐標系的原點重合,極軸與x軸的非負半軸重合,若曲線C1的方程為ρsin(θ+ ![]() )+2
)+2 ![]() =0,曲線C2的參數方程為
=0,曲線C2的參數方程為 ![]() (θ為參數).
(θ為參數).
(1)將C1的方程化為直角坐標方程;
(2)若點Q為C2上的動點,P為C1上的動點,求|PQ|的最小值.
 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,過點P分別做圓O的切線PA、PB和割線PCD,弦BE交CD于F,滿足P、B、F、A四點共圓.
(Ⅰ)證明:AE∥CD;
(Ⅱ)若圓O的半徑為5,且PC=CF=FD=3,求四邊形PBFA的外接圓的半徑.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣2|﹣|x+1|.
(1)解不等式f(x)>1.
(2)當x>0時,函數g(x)= ![]() (a>0)的最小值總大于函數f(x),試求實數a的取值范圍.
(a>0)的最小值總大于函數f(x),試求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓C: ![]() =1(α>b>0)經過點(
=1(α>b>0)經過點( ![]() ,
, ![]() ),且原點、焦點,短軸的端點構成等腰直角三角形.
),且原點、焦點,短軸的端點構成等腰直角三角形.
(1)求橢圓E的方程;
(2)是否存在圓心在原點的圓,使得該圓的任意一條切線(切線斜率存在)與橢圓C恒有兩個交點A,B.且 ![]() ?若存在,求出該圓的方程,若不存在說明理由.
?若存在,求出該圓的方程,若不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,EP交圓于E,C兩點,PD切圓于D,G為CE上一點且PG=PD,連接DG并延長交圓于點A,作弦AB垂直EP,垂足為F. 
(1)求證:BD⊥AD;
(2)若AC=BD,AB=6,求弦DE的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定圓![]() :
:![]() ,動圓
,動圓![]() 過點
過點![]()
![]() 且與圓
且與圓![]() 相切,記圓心
相切,記圓心![]() 的軌跡為
的軌跡為![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)已知直線![]()
![]() 交圓
交圓![]() 于
于![]() 兩點.
兩點.![]() 是曲線
是曲線![]() 上兩點,若四邊形
上兩點,若四邊形![]() 的對角線
的對角線![]() ,求四邊形
,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面立角坐標系![]() 中,過點
中,過點![]() 的圓的圓心
的圓的圓心![]() 在
在![]() 軸上,且與過原點傾斜角為
軸上,且與過原點傾斜角為![]() 的直線
的直線![]() 相切.
相切.
(1)求圓![]() 的標準方程;
的標準方程;
(2)點![]() 在直線
在直線![]() 上,過點
上,過點![]() 作圓
作圓![]() 的切線
的切線![]() 、
、![]() ,切點分別為
,切點分別為![]() 、
、![]() ,求經過
,求經過![]() 、
、![]() 、
、![]() 、
、![]() 四點的圓所過的定點的坐標.
四點的圓所過的定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】駐馬店市政府委托市電視臺進行“創建森林城市”知識問答活動,市電視臺隨機對該市15~65歲的人群抽取了![]() 人,繪制出如圖1所示的頻率分布直方圖,回答問題的統計結果如表2所示.
人,繪制出如圖1所示的頻率分布直方圖,回答問題的統計結果如表2所示.
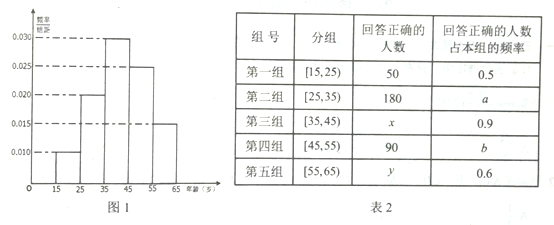
(1)分別求出![]() 的值;
的值;
(2)從第二、三、四、五組回答正確的人中用分層抽樣的方法抽取7人,則從第二、三、四、五組每組回答正確的人中應各抽取多少人?
(3)在(2)的條件下,電視臺決定在所抽取的7人中隨機選2人頒發幸運獎,求所抽取的人中第二組至少有1人獲得幸運獎的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解當下高二男生的身高狀況,某地區對高二年級男生的身高(單位: ![]() )進行了抽樣調查,得到的頻率分布直方圖如圖所示.已知身高在
)進行了抽樣調查,得到的頻率分布直方圖如圖所示.已知身高在![]() 之間的男生人數比身高在
之間的男生人數比身高在![]() 之間的人數少1人.
之間的人數少1人.

(1)若身高在![]() 以內的定義為身高正常,而該地區共有高二男生18000人,則該地區高二男生中身高正常的大約有多少人?
以內的定義為身高正常,而該地區共有高二男生18000人,則該地區高二男生中身高正常的大約有多少人?
(2)從所抽取的樣本中身高在![]() 和
和![]() 的男生中隨機再選出2人調查其平時體育鍛煉習慣對身高的影響,則所選出的2人中至少有一人身高大于185
的男生中隨機再選出2人調查其平時體育鍛煉習慣對身高的影響,則所選出的2人中至少有一人身高大于185![]() 的概率是多少?
的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com