【題目】為了解某社區居民購買水果和牛奶的年支出費用與購買食品的年支出費用的關系，隨機調查了該社區5戶家庭，得到如下統計數據表：
購買食品的年支出費用x（萬元） | 2.09 | 2.15 | 2.50 | 2.84 | 2.92 |
購買水果和牛奶的年支出費用y（萬元） | 1.25 | 1.30 | 1.50 | 1.70 | 1.75 |
根據上表可得回歸直線方程 
，其中 
，據此估計，該社區一戶購買食品的年支出費用為3.00萬元的家庭購買水果和牛奶的年支出費用約為（ ）
A.1.79萬元
B.2.55萬元
C.1.91萬元
D.1.94萬元
黃岡天天練口算題卡系列答案科目：高中數學 來源： 題型：
【題目】已知等差數列{an}的前n項和為Sn ， 且a3=3，S7=28，在等比數列{bn}中，b3=4，b4=8．
（1）求an及bn；
（2）設數列{anbn}的前n項和為Tn ， 求Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知在梯形ABCD中，∠ADC= 
，AB∥CD，PC⊥平面ABCD，CP=AB=2DC=2DA，點E在BP上，且EB=2PE． 
（1）求證：DP∥平面ACE；
（2）求二面角E﹣AC﹣P的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xoy中，圓的參數方程為 
（φ為參數），以坐標原點O為極點，x軸的正半軸為極軸的極坐標系中，直線l的極坐標方程為 
．
（1）將圓的參數方程化為普通方程，在化為極坐標方程；
（2）若點P在直線l上，當點P到圓的距離最小時，求點P的極坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）=ax3﹣x2﹣x+b（a，b∈R，a≠0），g（x）= 
（e是自然對數的底數），f（x）的圖象在x=﹣ 
處的切線方程為y= 
．
（1）求a，b的值；
（2）探究直線y= ．是否可以與函數g（x）的圖象相切？若可以，寫出切點的坐標，否則，說明理由；
（3）證明：當x∈（﹣∞，2]時，f（x）≤g（x）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某班級50名學生的考試分數x分布在區間[50，100）內，設分數x的分布頻率是f（x）且f（x）=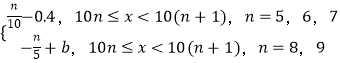 
，考試成績采用“5分制”，規定：考試分數在[50，60）內的成績記為1分，考試分數在[60，70）內的成績記為2分，考試分數在[70，80）內的成績記為3分，考試分數在[80，90）內的成績記為4分，考試分數在[90，100）內的成績記為5分．用分層抽樣的方法，現在從成績在1分，2分及3分的人中用分層抽樣隨機抽出6人，再從這6人中抽出3人，記這3人的成績之和為ξ（將頻率視為概率）．
（1）求b的值，并估計班級的考試平均分數；
（2）求P（ξ=7）；
（3）求ξ的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
sin（x+ 
）﹣ 
cos（x+ ），若存在x1 ， x2 ， x3 ， …，xn滿足0≤x1＜x2＜x3＜…＜xn≤6π，且|f（x1）﹣f（x2）|+|f（x2）﹣f（x3）|+… 
，則n的最小值為（ ）
A.6
B.10
C.8
D.12
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業生產甲，乙兩種產品均需用
兩種原料，已知生產1噸每種產品需用原料及每天原料的可用限額如下表所示，如果生產1噸甲，乙產品可獲利潤分別為3萬元、4萬元，則該企業可獲得最大利潤為__________萬元.
甲 | 乙 | 原料限額 | |
A(噸) | 3 | 2 | 12 |
B(噸) | 1 | 2 | 8 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
