
函數y=f(x)(x∈R)有下列命題:
①在同一坐標系中,y=f(x+1)與y=f(-x+1)的圖象關于直線x=1對稱;
②若f(2-x)=f(x),則函數y=f(x)的圖象關于直線x=1對稱;
③若f(x-1)=f(x+1),則函數y=f(x)是周期函數,且2是一個周期;
④若f(2-x)=-f(x),則函數y=f(x)的圖象關于(1,0)對稱,其中正確命題的序號是 .
②③④
【解析】對于①,y=f(x+1)的圖象由y=f(x)的圖象向左平移1個單位得到,y=f(-x+1)的圖象,由y=f(-x)的圖象向右平移1個單位得到,而y=f(x)與y=f(-x)關于y軸對稱,從而y=f(x+1)與y=f(-x+1)的圖象關于直線x=0對稱,故①錯;
對于②,由f(2-x)=f(x)將x換為x+1可得f(1-x)=f(1+x),從而②正確;
對于③,由f(x-1)=f(x+1)將x換為x+1可得,f(x+2)=f(x),從而③正確.
對于④,由f(2-x)=-f(x)同上可得f(1-x)=-f(1+x),從而④正確.
【誤區警示】解答本題時,易誤以為①正確,出錯的原因是混淆了兩個函數y=f(x+1)與y=f(-x+1)的圖象關系與一個函數y=f(x)滿足f(x+1)=f(-x+1)時圖象的對稱關系.


科目:高中數學 來源:2014年高考數學文二輪專題復習與測試解答題保分訓練練習卷(解析版) 題型:解答題
已知四棱錐P-ABCD的正視圖是一個底邊長為4,腰長為3的等腰三角形,如圖分別是四棱錐P-ABCD的側視圖和俯視圖.

(1)求證:AD⊥PC;
(2)求四棱錐P-ABCD的側面PAB的面積.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業(四)第二章第一節練習卷(解析版) 題型:選擇題
已知函數y=f(x)的圖象關于直線x=-1對稱,且當x∈(0,+∞)時,有f(x)=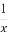 ,則當x∈(-∞,-2)時,f(x)的解析式為( )
,則當x∈(-∞,-2)時,f(x)的解析式為( )
(A)f(x)=-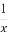 (B)f(x)=-
(B)f(x)=-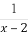
(C)f(x)=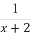 (D)f(x)=-
(D)f(x)=-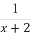
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業(四)第二章第一節練習卷(解析版) 題型:選擇題
若函數f(x)=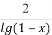 ,則函數f(x)的定義域是( )
,則函數f(x)的定義域是( )
(A)(1,+∞) (B)(0,1)∪(1,+∞)
(C)(-∞,-1)∪(-1,0) (D)(-∞,0)∪(0,1)
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業(六)第二章第三節練習卷(解析版) 題型:選擇題
設f(x)是定義在R上以2為周期的偶函數,已知x∈(0,1)時,f(x)=lo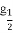 (1-x),則函數f(x)在(1,2)上( )
(1-x),則函數f(x)在(1,2)上( )
(A)是增函數,且f(x)<0
(B)是增函數,且f(x)>0
(C)是減函數,且f(x)<0
(D)是減函數,且f(x)>0
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業(六)第二章第三節練習卷(解析版) 題型:選擇題
已知函數f(x)=lg|x|,x∈R且x≠0,則f(x)是( )
(A)奇函數且在(0,+∞)上單調遞增
(B)偶函數且在(0,+∞)上單調遞增
(C)奇函數且在(0,+∞)上單調遞減
(D)偶函數且在(0,+∞)上單調遞減
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業(八)第二章第五節練習卷(解析版) 題型:選擇題
函數f(x)= 的定義域為( )
的定義域為( )
(A)(0,+∞) (B)(1,+∞)
(C)(0,1) (D)(0,1)∪(1,+∞)
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業(九)第二章第六節練習卷(解析版) 題型:選擇題
對于任意a∈[-1,1],函數f(x)=x2+(a-4)x+4-2a的值恒大于零,那么x的取值范圍是( )
(A)(1,3) (B)(-∞,1)∪(3,+∞)
(C)(1,2) (D)(3,+∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com