【題目】已知數列{an+1﹣2an}是公比為2的等比數列，其中a1=1，a2=4．
（1）證明：數列{ 
}是等差數列；
（2）求數列{an}的前n項和Sn；
（3）記Cn= 
（n≥2），證明： 
（ 
）n＜ 
+…+ 
≤1﹣（ ）n﹣1 ．
【答案】
（1）解：由已知得an+1﹣2an=（a2﹣2a1）2n﹣1=2n…2分
兩端同除 2n+1得： 
= 
，所以數列 { 
}是以首項為 ，公差為 的等差數列
（2）解：由 （1）知 = n，所以an=n2n﹣1，
Sn=120+221+…+n2n﹣1，
則2Sn=221+222…+（n﹣1）2n﹣1+n2n，
相減得：﹣Sn=120+21+…+2n﹣1﹣n2n，
所以﹣Sn= 
﹣n2n，
即Sn=（n﹣1）2n+1
（3）解：Cn=2n﹣2，（n≥2）
∵ 
= 
，
∴ 
+…+ 
+…+ 
= 
= ﹣ 
，
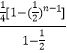當≥2時，∵2n+1﹣2n=2n≥4，∴2n+1﹣4≥2n 
，
∴ 
，
∴ +…+ 
+…+ 
= 
=1﹣ 
所以原不等式得證
【解析】（1）由已知得an+1﹣2an=（a2﹣2a1）2n﹣1=2n得： = ，即數列 { }是等差數列； （2）由 （1）知 = n，所以an=n2n﹣1 ， 利用錯位相減法可求數列{an}的前n項和Sn；（3）Cn=2n﹣2，（n≥2），利用 = 
證明即可．
【考點精析】利用數列的前n項和對題目進行判斷即可得到答案，需要熟知數列{an}的前n項和sn與通項an的關系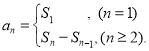
．
科目：高中數學 來源： 題型：
【題目】已知冪函數 
在（0，+∞）上為增函數，g（x）=f（x）+2 
（1）求m的值，并確定f（x）的解析式；
（2）對于任意x∈[1，2]，都存在x1 ， x2∈[1，2]，使得f（x）≤f（x1），g（x）≤g（x2），若f（x1）=g（x2），求實數t的值；
（3）若2xh（2x）+λh（x）≥0對于一切x∈[1，2]成成立，求實數λ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
，又
是一個常數，已知
或
時， 
只有一個實根，當
時， 
有三個相異實根，給出下列命題：
①
和
有一個相同的實根；
②
和
有一個相同的實根；
③
的任一實根大于
的任一實根；
④
的任一實根小于
的任一實根．
其中正確命題的個數為（ ）
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系
中，以
為極點，
軸正半軸為極軸建立極坐標系，圓
的極坐標方程為
，直線
的參數方程為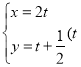
為參數），直線和圓交于
兩點，
是圓上不同于的任意一點．
（1）求圓心的極坐標；
（2）求點到直線的距離的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以平面直角坐標系
的原點為極點， 
軸正半軸為極軸且取相同的單位長度建立極坐標系．已知點
的參數方程為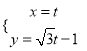
（
為參數），點
在曲線
上．
（1）求在平面直角坐標系
中點
的軌跡方程和曲線
的普通方程；
（2）求
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x3+bx2+cx的導函數圖象關于直線x=2對稱
（1）求b值；
（2）若f（x）在x=t處取得極小值，記此極小值為g（t），求g（t）的定義域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=lnx﹣ax2+（2﹣a）x． （Ⅰ）討論f（x）的單調性；
（Ⅱ）設a＞0，證明：當0＜x＜ 
時，f（ +x）＞f（ ﹣x）；
（Ⅲ）若函數y=f（x）的圖象與x軸交于A，B兩點，線段AB中點的橫坐標為x0 ， 證明：f′（x0）＜0．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
