
(Ⅰ)討論f(x)的奇偶性;
(Ⅱ)求f(x)的最小值.
(21)本小題主要考查函數的概念、函數的奇偶性和最小值等基礎知識,考查分類討論的思想和邏輯思維能力.
解:
(Ⅰ)當a=0時,函數f(-x)=(-x)2+|-x|+1=f(x),此時f(x)為偶函數.
當a≠0時,f(a)=a2+1,f(-a)=a2+2|a|+1,f(-a)≠f(a),f(-a)≠-f(a).
此時函數f(x)既不是奇函數,也不是偶函數.
(Ⅱ)(i)當x≤a時,函數f(x)=x2-x+a+1=(x-![]() )2+a+
)2+a+![]() .
.
若a≤![]() ,則函數f(x)在(-∞,a]上單調遞減,從而,函數
,則函數f(x)在(-∞,a]上單調遞減,從而,函數
f(x)在(-∞,a]上的最小值為f(a)=a2+1.
若a>![]() ,則函數f(x)在(-∞,a]上的最小值為
,則函數f(x)在(-∞,a]上的最小值為
f(![]() )=
)=![]() +a,且f(
+a,且f(![]() )≤f(a).
)≤f(a).
(ⅱ)當x≥a時,函數f(x)=x2+x-a+1=(x+![]() )2-a+
)2-a+![]() .
.
若a≤-![]() ,則函數f(x)在[a,+∞)上的最小值為f(-
,則函數f(x)在[a,+∞)上的最小值為f(-![]() )=
)=![]() -a,且f(-
-a,且f(-![]() )≤f(a).
)≤f(a).
若a>-![]() ,則函數f(x)在[a,+∞)上單調遞增,從而,函數f(x)在[a,+∞)上的
,則函數f(x)在[a,+∞)上單調遞增,從而,函數f(x)在[a,+∞)上的
最小值為f(a)=a2+1.
綜上,當a≤-![]() 時,函數f(x)的最小值是
時,函數f(x)的最小值是![]() -a.
-a.
當-![]() <a≤
<a≤![]() 時,函數f(x)的最小值是a2+1.
時,函數f(x)的最小值是a2+1.
當a>![]() 時,函數f(x)的最小值是a+
時,函數f(x)的最小值是a+![]() .
.


科目:高中數學 來源: 題型:
| 2 | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| 1+2x |
| 2 |
| 1+2x |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省南京市江寧高級中學高三(上)期中數學試卷(解析版) 題型:解答題
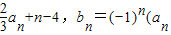 -3n+21),其中λ為實數,n為正整數.Sn為數列{bn}的前n項和.
-3n+21),其中λ為實數,n為正整數.Sn為數列{bn}的前n項和.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com