
【題目】設函數f(x)=|x+ ![]() |+|x﹣a+1|(a>0是常數).
|+|x﹣a+1|(a>0是常數).
(Ⅰ)證明:f(x)≥1;
(Ⅱ)若f(3)< ![]() ,求a的取值范圍.
,求a的取值范圍.
【答案】解:(Ⅰ)函數f(x)=|x+ ![]() |+|x﹣a+1|≥|
|+|x﹣a+1|≥| ![]() |=|
|=| ![]() |
|
∵a>0,
∴ ![]() ,當且僅當a=1時取等號.
,當且僅當a=1時取等號.
∴ ![]() ≥1
≥1
故得:函數f(x)=| ![]() |≥1,即f(x)≥1;
|≥1,即f(x)≥1;
(Ⅱ)當x=3時,可得f(3)=|3+ ![]() |+|3﹣a+1|
|+|3﹣a+1| ![]() ,
,
∵a>0,
可得:3+ ![]() +|4﹣a|
+|4﹣a| ![]()
|4﹣a|< ![]() ,
,
∴ ![]() ,且
,且 ![]() ,
,
解得: ![]()
故得a的取值范圍是(2, ![]() ).
).
【解析】(Ⅰ)利用絕對值不等式證明即可.(Ⅱ)將x=3帶入,可得f(3)=|3+ ![]() |+|3﹣a+1|
|+|3﹣a+1| ![]() ,去絕對值,即可得答案.
,去絕對值,即可得答案.
【考點精析】關于本題考查的絕對值不等式的解法,需要了解含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規律:關鍵是去掉絕對值的符號才能得出正確答案.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知點![]() 分別是Δ
分別是Δ![]() 的邊
的邊![]() 的中點,連接
的中點,連接![]() .現將
.現將![]() 沿
沿![]() 折疊至Δ
折疊至Δ![]() 的位置,連接
的位置,連接![]() .記平面
.記平面 ![]() 與平面
與平面 ![]() 的交線為
的交線為![]() ,二面角
,二面角![]() 大小為
大小為![]() .
.


(1)證明: ![]()
(2)證明: ![]()
(3)求平面![]() 與平面
與平面 ![]() 所成銳二面角大小.
所成銳二面角大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個命題中,正確命題的個數是( )
①命題“若x=y,則sinx=siny”的逆否命題是真命題;
②已知α,β是不同的平面,m,n是不同的直線,m∥α,n∥β,α⊥β,則m⊥n;
③直線l1:2ax+y+1=0,l2:x+2ay+2=0,l1∥l2的充要條件是 ![]() ;
;
④ ![]() .
.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,四邊形AMNC為等腰梯形,△ABC為直角三角形,平面AMNC與平面ABC垂直,AB=BC,AM=CN,點O、D、E分別是AC、MN、AB的中點.過點E作平行于平面AMNC的截面分別交BD、BC于點F、G,H是FG的中點.
(Ⅰ)證明:OB⊥EH;
(Ⅱ)若直線BH與平面EFG所成的角的正弦值為 ![]() ,求二面角D﹣AC﹣H的余弦值.
,求二面角D﹣AC﹣H的余弦值.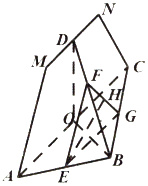
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中, ![]() 平面
平面![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 和
和![]() 的中點,
的中點, ![]() 為側棱
為側棱![]() 上的動點.
上的動點.

(![]() )求證:平面
)求證:平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() 為線段
為線段![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() .
.
(![]() )試判斷直線
)試判斷直線![]() 與平面
與平面![]() 是否能夠垂直.若能垂直,求
是否能夠垂直.若能垂直,求![]() 的值,若不能垂直,請說明理由.
的值,若不能垂直,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com