【題目】甲、乙二人做射擊游戲，甲、乙射擊擊中與否是相互獨(dú)立事件．規(guī)則如下：若射擊一次擊中，則原射擊人繼續(xù)射擊；若射擊一次不中，就由對方接替射擊．已知甲、乙二人射擊一次擊中的概率均為
，且第一次由甲開始射擊．①求前3次射擊中甲恰好擊中2次的概率____________；②求第4次由甲射擊的概率________．
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】長方體
中， 
， 
分別是
， 
的中點(diǎn)， 
， 
．
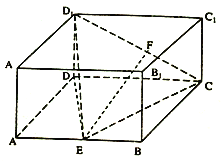
（Ⅰ）求證： 
平面
；
（Ⅱ）求證：平面
平面
；
（Ⅲ）在線段
上是否存在一點(diǎn)
，使得二面角
為
，若存在，求
的值；若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
（
）的離心率為
，短軸的一個(gè)端點(diǎn)為
.過橢圓左頂點(diǎn)
的直線
與橢圓的另一交點(diǎn)為
.
（1）求橢圓的方程；
（2）若
與直線
交于點(diǎn)
，求
的值；
（3）若
，求直線
的傾斜角.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】選修4-5：不等式選講
已知函數(shù)
.
（1）當(dāng)
時(shí)，求
的最小值；
（2）存在
時(shí)，使得不等式
成立，求實(shí)數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】為了研究一種昆蟲的產(chǎn)卵數(shù)
和溫度
是否有關(guān)，現(xiàn)收集了7組觀測數(shù)據(jù)列于下表中，并作出了散點(diǎn)圖，發(fā)現(xiàn)樣本點(diǎn)并沒有分布在某個(gè)帶狀區(qū)域內(nèi)，兩個(gè)變量并不呈線性相關(guān)關(guān)系，現(xiàn)分別用模型①：
與模型②：
作為產(chǎn)卵數(shù)
和溫度
的回歸方程來建立兩個(gè)變量之間的關(guān)系.
溫度 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
產(chǎn)卵數(shù) | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
| 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
| 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
|
|
|
|
26 | 692 | 80 | 3.57 |
|
|
|
|
1157.54 | 0.43 | 0.32 | 0.00012 |
其中
， 
， 
，
附：對于一組數(shù)據(jù)
，其回歸直線
的斜率和截距的最小二乘估計(jì)分別為：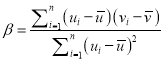 
， 
.
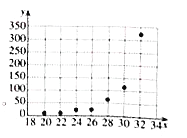
（1）在答題卡中分別畫出
關(guān)于
的散點(diǎn)圖、
關(guān)于
的散點(diǎn)圖，根據(jù)散點(diǎn)圖判斷哪一個(gè)模型更適宜作為回歸方程類型？（給出判斷即可，不必說明理由）.
（2）根據(jù)表中數(shù)據(jù)，分別建立兩個(gè)模型下建立
關(guān)于
的回歸方程；并在兩個(gè)模型下分別估計(jì)溫度為
時(shí)的產(chǎn)卵數(shù).（
與估計(jì)值均精確到小數(shù)點(diǎn)后兩位）（參考數(shù)據(jù)： 
， 
， 
）
（3）若模型①、②的相關(guān)指數(shù)計(jì)算得分分別為
， 
，請根據(jù)相關(guān)指數(shù)判斷哪個(gè)模型的擬合效果更好.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知點(diǎn)
是長軸長為
的橢圓
： 
上異于頂點(diǎn)的一個(gè)動(dòng)點(diǎn)， 
為坐標(biāo)原點(diǎn)， 
為橢圓的右頂點(diǎn)，點(diǎn)
為線段
的中點(diǎn)，且直線
與
的斜率之積恒為
.
（1）求橢圓
的方程；
（2）設(shè)過左焦點(diǎn)
且不與坐標(biāo)軸垂直的直線
交橢圓于
兩點(diǎn)，線段
的垂直平分線與
軸交于點(diǎn)
，點(diǎn)
橫坐標(biāo)的取值范圍是
，求
的最小值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列命題中錯(cuò)誤的是（ ）
A. 如果平面
外的直線
不平行于平面
，則平面
內(nèi)不存在與
平行的直線
B. 如果平面
平面
，平面
平面
， 
，那么直線
平面
C. 如果平面
平面
，那么平面
內(nèi)所有直線都垂直于平面
D. 一條直線與兩個(gè)平行平面中的一個(gè)平面相交，則必與另一個(gè)平面相交
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】隨著手機(jī)的發(fā)展，“微信”越來越成為人們交流的一種方式.某機(jī)構(gòu)對“使用微信交流”的態(tài)度進(jìn)行調(diào)查，隨機(jī)抽取了50人，他們年齡的頻數(shù)分布及對“使用微信交流”贊成人數(shù)如下表.
年齡（單位：歲） | [15,25） | [25,35） | [35,45） | [45,55） | [55,65） | [65,75） |
頻數(shù) | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數(shù) | 5 | 10 | 12 | 7 | 2 | 1 |
（Ⅰ）若以“年齡45歲為分界點(diǎn)”，由以上統(tǒng)計(jì)數(shù)據(jù)完成下面
列聯(lián)表，并判斷是否有99%的把握認(rèn)為“使用微信交流”的態(tài)度與人的年齡有關(guān)；
年齡不低于45歲的人數(shù) | 年齡低于45歲的人數(shù) | 合計(jì) | |
贊成 | |||
不贊成 | |||
合計(jì) |
（Ⅱ）若從年齡在[25,35）和[55,65）的被調(diào)查人中按照分層抽樣的方法選取6人進(jìn)行追蹤調(diào)查，并給予其中3人“紅包”獎(jiǎng)勵(lì)，求3人中至少有1人年齡在[55,65）的概率.
參考數(shù)據(jù)如下：
附臨界值表：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
的觀測值： 
（其中
）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
．
（Ⅰ）過原點(diǎn)作曲線
的切線，求切線方程；
（Ⅱ）當(dāng)
時(shí)，討論曲線
與曲線
公共點(diǎn)的個(gè)數(shù)．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com
