
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)設![]() ,當
,當![]() 時,對任意
時,對任意![]() ,存在
,存在![]() ,使得
,使得![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)當![]() 時,單調減區間是
時,單調減區間是![]() ,單調增區間是
,單調增區間是![]() ,
,![]() ;當
;當![]() 時,單調增區間是
時,單調增區間是![]() ,沒有單調減區間;(2)
,沒有單調減區間;(2)![]() .
.
【解析】
(1)先求函數的定義域,利用函數的導函數![]() ,得
,得![]() 或
或![]() ,當
,當![]() 時,分
時,分![]() ,
,![]() 討論即可得到答案;
討論即可得到答案;
(2)當![]() 時,由(1)知
時,由(1)知![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
從而![]() 在
在![]() 上的最小值為
上的最小值為![]() ,由題意得
,由題意得![]() ,即
,即![]() ,令
,令![]() ,求新函數
,求新函數![]() 的最大值即可得實數
的最大值即可得實數![]() 的取值范圍.
的取值范圍.
(1)函數![]() 的定義域為
的定義域為![]() ,
,
![]()
![]() ,
,
由![]() ,得
,得![]() 或
或![]() .
.
當![]() 即
即![]() 時,由
時,由![]() 得
得![]() ,
,
由![]() 得
得![]() 或
或![]() ;
;
當![]() 即
即![]() 時,當
時,當![]() 時都有
時都有![]() ;
;
![]() 當
當![]() 時,單調減區間是
時,單調減區間是![]() ,單調增區間是
,單調增區間是![]() ,
,![]() ;
;
當![]() 時,單調增區間是
時,單調增區間是![]() ,沒有單調減區間.
,沒有單調減區間.
(2)當![]() 時,由(1)知
時,由(1)知![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
從而![]() 在
在![]() 上的最小值為
上的最小值為![]() .
.
對任意![]() ,存在
,存在![]() ,使得
,使得![]() ,
,
即存在![]() ,使
,使![]() 的值不超過
的值不超過![]() 在區間
在區間![]() 上的最小值
上的最小值![]() .
.
由![]() ,
,![]() .
.
令![]() ,則當
,則當![]() 時,
時,![]() .
.
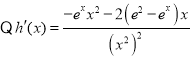
![]() ,
,
當![]() 時
時![]() ;當
;當![]() 時,
時,![]()
![]() ,
,![]() .
.
故![]() 在
在![]() 上單調遞減,
上單調遞減,
從而![]() ,
,
從而![]() .
.


 應用題作業本系列答案
應用題作業本系列答案科目:高中數學 來源: 題型:
【題目】已知對于任意![]() ,函數
,函數![]()
![]() 與
與![]()
![]() 的圖像在
的圖像在![]() 上都有三個不同交點.
上都有三個不同交點.
(1)寫出![]() 的解析式,并求函數的最大值及此時的x的取值;
的解析式,并求函數的最大值及此時的x的取值;
(2)若函數![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,且
上單調遞減,且![]() ,求
,求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“辛卜生公式”給出了求幾何體體積的一種計算方法:夾在兩個平行平面之間的幾何體,如果被平行于這兩個平面的任何平面所截,截得的截面面積是截面高(不超過三次)的多項式函數,那么這個幾何體的體積,就等于其上底面積、下底面積與四倍中截面面積的和乘以高的六分之一.即:![]() ,式中
,式中![]() ,
,![]() ,
,![]() ,
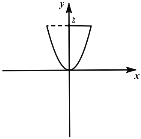
,![]() 依次為幾何體的高,下底面積,上底面積,中截面面積.如圖,現將曲線
依次為幾何體的高,下底面積,上底面積,中截面面積.如圖,現將曲線![]() 與直線
與直線![]() 及
及![]() 軸圍成的封閉圖形繞
軸圍成的封閉圖形繞![]() 軸旋轉一周得到一個幾何體.利用辛卜生公式可求得該幾何體的體積
軸旋轉一周得到一個幾何體.利用辛卜生公式可求得該幾何體的體積![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 上的一點
上的一點![]() 到其左頂點
到其左頂點![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(
兩點(![]() 與點
與點![]() 不重合),若以
不重合),若以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ,試證明:直線
,試證明:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題中真命題是![]()
![]()
A. 同垂直于一直線的兩條直線互相平行
B. 底面各邊相等,側面都是矩形的四棱柱是正四棱柱
C. 過空間任一點與兩條異面直線都垂直的直線有且只有一條
D. 過球面上任意兩點的大圓有且只有一個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義函數![]() ,數列
,數列![]() 滿足
滿足![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 及
及![]() ;
;
(2)若![]() 且數列
且數列![]() 為周期函數,且最小正周期
為周期函數,且最小正周期![]() ,求
,求![]() 的值;
的值;
(3)是否存在![]() ,使得
,使得![]() 成等比數列?若存在,求出所有這樣的
成等比數列?若存在,求出所有這樣的![]() ,若不存在,說明理由.
,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】綠水青山就是金山銀山.近年來,祖國各地依托本地自然資源,打造旅游產業,旅游業正蓬勃發展.景區與游客都應樹立尊重自然、順應自然、保護自然的生態文明理念,合力使旅游市場走上規范有序且可持續的發展軌道.某景區有一個自愿消費的項目:在參觀某特色景點入口處會為每位游客拍一張與景點的合影,參觀后,在景點出口處會將剛拍下的照片打印出來,游客可自由選擇是否帶走照片,若帶走照片則需支付20元,沒有被帶走的照片會收集起來統一銷毀.該項目運營一段吋間后,統計出平均只有三成的游客會選擇帶走照片,為改善運營狀況,該項目組就照片收費與游客消費意愿關系作了市場調研,發現收費與消費意愿有較強的線性相關性,并統計出在原有的基礎上,價格每下調1元,游客選擇帶走照片的可能性平均增加0.05,假設平均每天約有5000人參觀該特色景點,每張照片的綜合成本為5元,假設每個游客是否購買照片相互獨立.
(1)若調整為支付10元就可帶走照片,該項目每天的平均利潤比調整前多還是少?
(2)要使每天的平均利潤達到最大值,應如何定價?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列A:![]() ,
,![]() ,…
,…![]() (
(![]() ).如果對小于
).如果對小于![]() (
(![]() )的每個正整數
)的每個正整數![]() 都有
都有![]() <
<![]() ,則稱
,則稱![]() 是數列A的一個“G時刻”.記“
是數列A的一個“G時刻”.記“![]() 是數列A的所有“G時刻”組成的集合.
是數列A的所有“G時刻”組成的集合.
(1)對數列A:-2,2,-1,1,3,寫出![]() 的所有元素;
的所有元素;
(2)證明:若數列A中存在![]() 使得
使得![]() >
>![]() ,則
,則![]() ;
;
(3)證明:若數列A滿足![]() -
-![]() ≤1(n=2,3, …,N),則
≤1(n=2,3, …,N),則![]() 的元素個數不小于
的元素個數不小于![]() -
-![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com