
已知函數 的一系列對應值如下表:
的一系列對應值如下表:
 |  |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |
 的一個解析式;
的一個解析式; 周期為
周期為 ,當
,當 時,
時, 恰有兩個不同的解,求實數
恰有兩個不同的解,求實數 的取值范圍.
的取值范圍. (1)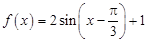 ;(2)實數
;(2)實數 的取值范圍為
的取值范圍為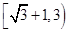 .
.
解析試題分析:(1)根據表格提供的數據,求出周期T,注意:三角函數的周期等于圖象上相鄰兩個最低點的橫坐標之差的絕對值,解出ω,由A>0知函數的最大值為A+B,最小值為-A+B,利用已知最小值、最大值可求出A、B,結合周期求出φ,可求函數 的一個解析式.
的一個解析式.
(2)函數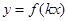 (k>0)周期為
(k>0)周期為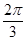 ,求出k,x∈[0,
,求出k,x∈[0, ],推出3x?
],推出3x? 的范圍,畫出圖象,數形結合容易求出m的范圍.
的范圍,畫出圖象,數形結合容易求出m的范圍.
試題解析:(1)設 的最小正周期為
的最小正周期為 ,得
,得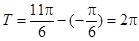 , 2分
, 2分
由 , 得
, 得 ,又
,又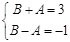 ,解得
,解得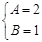 4分
4分
令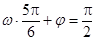 ,即
,即 ,解得
,解得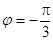 , 5分
, 5分
∴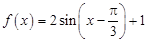 6分
6分
(2)∵函數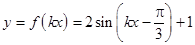 的周期為
的周期為 ,
,
又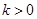 , ∴
, ∴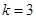 , 7分
, 7分
令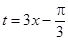 ,∵
,∵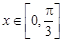 , ∴
, ∴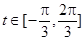 , .8分
, .8分
如圖,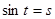 在
在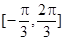 上有兩個不同的解,則
上有兩個不同的解,則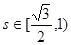 , 10分
, 10分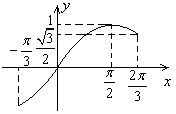
∴方程 在
在 時恰好有兩個不同的解,
時恰好有兩個不同的解,
則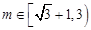 ,即實數
,即實數 的取值范圍是
的取值范圍是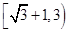 12分
12分
考點:1.由三角函數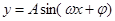 的部分圖象求解析式;2.三角函數的周期性及求法.
的部分圖象求解析式;2.三角函數的周期性及求法.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com