
【題目】給定數列![]() ,對
,對![]() ,該數列前
,該數列前![]() 項的最大值記為
項的最大值記為![]() ,后
,后![]() 項
項![]() 的最小值記為
的最小值記為![]() ,
,![]() .
.
(1)設數列![]() 為3,4,7,5,2,寫出
為3,4,7,5,2,寫出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)設![]() 是
是![]() ,公比
,公比![]() 的等比數列,證明:
的等比數列,證明:![]() 成等比數列;
成等比數列;
(3)設![]() ,證明:
,證明:![]() 的充分必要條件為
的充分必要條件為![]() 是公差為
是公差為![]() 的等差數列.
的等差數列.
【答案】(1)見解析;(2)見解析;(3)見解析
【解析】
(1)可根據題意來逐步代入計算;(2)根據a1>0,公比q>1,可判斷出數列{an}是一個單調遞增的等比數列,則可逐步代入Ai與Bi的值進行計算,再證明出d1,d2,d3,…dn﹣1成等比數列.(3)先證充分性:因為m>0可得![]() 單增,則
單增,則![]() ,
,![]() 可得
可得![]() ;再證必要性,先利用反證法說明數列
;再證必要性,先利用反證法說明數列![]() 中不存在
中不存在![]() 使
使![]() ,則可說明
,則可說明![]() ,
,![]() ,則得
,則得![]() ,從而證得結論.
,從而證得結論.
(1)由題意,可知:
①當i=1時,A1=3,B1=2,d1=A1﹣B1=3﹣2=1;
②當i=2時,A2=4,B2=2,d2=A2﹣B2=4﹣2=2;
③當i=3時,A3=7,B3=2,d3=A3﹣B3=7﹣2=5;
④當i=4時,A4=7,B4=2,d4=A4﹣B4=7﹣2=5.
(2)由題意,可知:
∵a1>0,公比q>1,
∴數列{an}是一個單調遞增的等比數列.
∴①當i=1時,A1=a1,B1=a2,d1=A1﹣B1=a1﹣a2=a1(1﹣q);
②當i=2時,A2=a2,B2=a3,d2=A2﹣B2=a2﹣a3=a1(1﹣q)q;
③當i=3時,A3=a3,B3=a4,d3=A3﹣B3=a3﹣a4=a1(1﹣q)q2;
…
∴對![]() ,
,
![]()
![]() .
.
因此![]() 且
且![]()
![]() ,
,
∴![]() 為首項為a1(1﹣q),公比為q的等比數列.
為首項為a1(1﹣q),公比為q的等比數列.
(3)充分性:若![]() 是公差為
是公差為![]() 的等差數列,則
的等差數列,則![]() ,
,
因為![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
必要性:若![]() ,
,![]() .
.
假設![]() 是第一個使
是第一個使![]() 的項,
的項,
則![]() ,這與
,這與![]() 相矛盾,故
相矛盾,故![]() ∴
∴![]()
![]() ,即
,即![]() ,故
,故![]() 是公差為
是公差為![]() 的等差數列.
的等差數列.


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案 導學與測試系列答案
導學與測試系列答案科目:高中數學 來源: 題型:
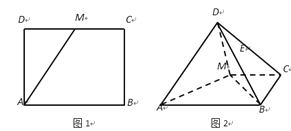
【題目】長方形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 中點(圖1).將△
中點(圖1).將△![]() 沿
沿![]() 折起,使得
折起,使得![]() (圖2)在圖2中:
(圖2)在圖2中:
(1)求證:平面![]()
![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存點
上是否存點![]() ,使得二面角
,使得二面角![]() 為大小為
為大小為![]() ,說明理由.
,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人有樓房一幢,室內總面積為![]() ,擬分割成兩類房間作為旅游客房,有關的數據如下表:
,擬分割成兩類房間作為旅游客房,有關的數據如下表:
大房間 | 小房間 | |
每間的面積 |
|
|
每間裝修費 |
| 6000元 |
每天每間住人數 | 5人 | 3人 |
每天每人住宿費 | 80元 | 100元 |
如果他只能籌款80000元用于裝修,且游客能住滿客房,他應隔出大房間和小房間各多少間,能獲得的住宿總收入最多?每天獲得的住宿總收入最多是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代數學著作《算法統宗》中有這樣一個問題:“三百七十八里關,初行健步不為難,次日腳痛減一半,六朝才得到其關……”其大意為:“某人從距離關口三百七十八里處出發,第一天走得輕快有力,從第二天起,由于腳痛,每天走的路程為前一天的一半,共走了六天到達關口……” 那么該人第一天走的路程為______________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
(1)直線![]() 與線段
與線段![]() 相交,其中
相交,其中![]() ,
,![]() ,則
,則![]() 的取值范圍是
的取值范圍是![]() ;
;
(2)點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]() ,則
,則![]() 的坐標為
的坐標為![]() ;
;
(3)圓![]() 上恰有
上恰有![]() 個點到直線
個點到直線![]() 的距離為
的距離為![]() ;
;
(4)直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,則以
兩點,則以![]() 為直徑的圓恰好與直線
為直徑的圓恰好與直線![]() 相切.
相切.
其中正確的命題有_________.(把所有正確的命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() ,過右焦點
,過右焦點![]() 作直線
作直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() 的周長為
的周長為![]() ,點
,點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 、
、![]() 的斜率
的斜率![]() ,
,![]() ,請問
,請問![]() 是否為定值?若是定值,求出其定值;若不是,說明理由.
是否為定值?若是定值,求出其定值;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著移動互聯網的發展,與餐飲美食相關的手機APP軟件層出不窮.現從某市使用A和B兩款訂餐軟件的商家中分別隨機抽取100個商家,對它們的“平均送達時間”進行統計,得到頻率分布直方圖如下.


![]()
![]()
(1)已知抽取的100個使用A款訂餐軟件的商家中,甲商家的“平均送達時間”為18分鐘。現從使用A款訂餐軟件的商家中“平均送達時間”不超過20分鐘的商家中隨機抽取3個商家進行市場調研,求甲商家被抽到的概率;
(2)試估計該市使用A款訂餐軟件的商家的“平均送達時間”的眾數及平均數;
(3)如果以“平均送達時間”的平均數作為決策依據,從A和B兩款訂餐軟件中選擇一款訂餐,你會選擇哪款?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列![]() 的公差d大于0,前n項的和為
的公差d大于0,前n項的和為![]() .已知
.已知![]() =18,
=18,![]() ,
,![]() ,
,![]() 成等比數列.
成等比數列.
(1)求![]() 的通項公式;
的通項公式;
(2)若對任意的![]() ,都有k(
,都有k(![]() +18)≥
+18)≥![]() 恒成立,求實數k的取值范圍;
恒成立,求實數k的取值范圍;
(3)設![]() (
(![]() ).若s,t
).若s,t![]() ,s>t>1,且
,s>t>1,且![]() ,求s,t的值.
,求s,t的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com