【題目】如圖，四棱錐
中，
⊥平面
，底面為正方形，
為
的中點，
.
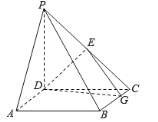
（1）求證：
；
（2）
邊上是否存在一點
，使得
//平面
？若存在，求
的長，若不存在，請說明理由.
【答案】（1）見解析；（2）23.
【解析】分析：（1）要證明
，需證
面
，需證：
，用分析法書寫即可。
（2）連結AC,取AC中點O,連結EO,GO,延長GO交AD于點M,則PA∥平面MEG，再求解
詳解：(Ⅰ)證明：∵PD⊥平面A
CD，∴PD⊥BC
又∵ABCD是正方形∴BC⊥CD
∵PD∩CD=D
∴BC⊥平面PCD
又∵PC面PBC
∴PC⊥BC
（2）連結AC,取AC中點O,連結EO,GO,延長GO交AD于點M,則PA∥平面MEG
下面證明之
∵E為PC的中點，O是AC的中點，
∴EO∥PA,
又∵EO平面MEG，PA平面MEG
∴PA∥平面MEG
在正方形ABCD中,∵O是AC的中點,∴△OCG≌△OAM，
∴AM=CG=23,∴所求AM的長為23.
名校名師培優(yōu)作業(yè)本加核心試卷系列答案
全程金卷系列答案科目：高中數(shù)學 來源： 題型：
【題目】某市場調(diào)查發(fā)現(xiàn)，某種產(chǎn)品在投放市場的30天中，其銷售價格P（元）和時間t（天）（t∈N）的關系如圖所示 
（1）寫出銷售價格P（元）和時間t（天）的函數(shù)解析式；
（2）若日銷售量Q（件）與時間t（天）的函數(shù)關系是Q=﹣t+40（0≤t≤30，t∈N），求該商品的日銷售金額y（元）與時間t（天）的函數(shù)解析式；
（3）問該產(chǎn)品投放市場第幾天時，日銷售金額最高？最高值為多少元？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】（本小題滿分14分）某學校為了支持生物課程基地研究植物生長，計劃利用學校空地建造一間室內(nèi)面積為900m2的矩形溫室，在溫室內(nèi)劃出三塊全等的矩形區(qū)域，分別種植三種植物，相鄰矩形區(qū)域之間間隔1m，三塊矩形區(qū)域的前、后與內(nèi)墻各保留 1m 寬的通道，左、右兩塊矩形區(qū)域分別與相鄰的左右內(nèi)墻保留 3m 寬的通道，如圖．設矩形溫室的室內(nèi)長為
（m），三塊種植植物的矩形區(qū)域的總面積為
（m2）．
（1）求
關于
的函數(shù)關系式；
（2）求
的最大值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知公差不為0的等差數(shù)列{an}的首項a1為a(a∈R)．設數(shù)列的前n項和為Sn，且
，
，
成等比數(shù)列．
(1)求數(shù)列{an}的通項公式及Sn；
(2)記
，
.當n≥2時，求An與Bn．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】給出以下命題：
（1）若
：
；
：
，則
為真，
為假，
為真
（2）“
”是“曲線
表示橢圓”的充要條件
（3）命題“若
，則
”的否命題為：“若，則
”
（4）如果將一組數(shù)據(jù)中的每一個數(shù)都加上同一個非零常數(shù)，那么這組數(shù)據(jù)的平均數(shù)和方差都改變；
則正確命題有（ ）個
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設等差數(shù)列{an}的前n項和為Sn ， 且滿足S17＞0，S18＜0，則 
， 
，…， 
中最大的項為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面內(nèi)，定點A，B，C，D滿足| 
|=| 
|=| 
|，| || |=| || |=| || |=﹣4，動點P，M滿足| 
|=2， 
= 
，則| 
|的最大值是 ．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知等差數(shù)列{an}的公差不為零，a1＝25，且a1，a11，a13成等比數(shù)列．
(1)求{an}的通項公式；
(2)求a1＋a4＋a7＋…＋a3n－2.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
