
【題目】如圖,在正方體ABCD﹣A1B1C1D1中, 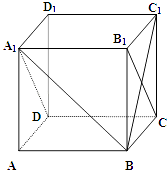
(1)證明:BC1⊥面A1B1CD;
(2)求直線A1B和平面A1B1CD所成的角.
【答案】
(1)解:連接B1C交BC1于點O,連接A1O.
在正方體ABCD﹣A1B1C1D1中
因為A1B1⊥平面BCC1B1.
所以A1B1⊥BC1.
又∵BC1⊥B1C,又BC1∩B1C=O
∴BC1⊥平面A1B1CD

(2)解:因為BC1⊥平面A1B1CD,所以A1O為斜線A1B在平面A1B1CD內的射影,所以∠BA1O為A1B與平面A1B1CD所成的角.設正方體的棱長為a
在RT△A1BO中,A1B= ![]() a,BO=
a,BO= ![]() a,所以BO=
a,所以BO= ![]() A1B,∠BA1O=30°,
A1B,∠BA1O=30°,
即直線A1B和平面A1B1CD所成的角為30°
【解析】(1)要證BC1⊥面A1B1CD;應通過證明A1B1⊥BC1 . BC1⊥B1C兩個關系來實現,兩關系容易證明.(2)因為BC1⊥平面A1B1CD,所以A1O為斜線A1B在平面A1B1CD內的射影,所以∠BA1O為A1B與平面A1B1CD所成的角.在RT△A1BO中求解即可.
【考點精析】關于本題考查的直線與平面垂直的判定和空間角的異面直線所成的角,需要了解一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想;已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則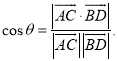 才能得出正確答案.
才能得出正確答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某同學用“五點法”畫函數f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一個周期內的圖象時,列表并填入了部分數據,如表:
)在某一個周期內的圖象時,列表并填入了部分數據,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)請將上表數據補充完整,填寫在相應位置,并直接寫出函數f(x)的解析式;
(2)將y=f(x)圖象上所有點向左平行移動θ(θ>0)個單位長度,得到y=g(x)的圖象.若y=g(x)圖象的一個對稱中心為( ![]() ,0),求θ的最小值.
,0),求θ的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=xsinx,x1、x2∈[﹣ ![]() ,
, ![]() ],且f(x1)>f(x2),則下列結論必成立的是( )
],且f(x1)>f(x2),則下列結論必成立的是( )
A.x1>x2
B.x1+x2>0
C.x1<x2
D.x12>x22
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 與
與![]() 的圖象關于
的圖象關于![]() 軸對稱,當函數
軸對稱,當函數![]() 和
和![]() 在區間
在區間![]() 同時遞增或同時遞減時,把區間
同時遞增或同時遞減時,把區間![]() 叫做函數
叫做函數![]() 的“不動區間”.若區間
的“不動區間”.若區間![]() 為函數
為函數![]() 的“不動區間”,則實數
的“不動區間”,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() )的圖象如圖所示,直線x=
)的圖象如圖所示,直線x= ![]() ,x=
,x= ![]() 是其兩條對稱軸.
是其兩條對稱軸. 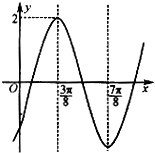
(1)求函數f(x)的解析式及單調區間;
(2)若f(α)= ![]() ,且
,且 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是定義在
是定義在![]() 上的奇函數,當
上的奇函數,當![]() 時,
時, ![]() (
(![]() ),且曲線
),且曲線![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 平行.
平行.
(1)求![]() 的值及函數
的值及函數![]() 的解析式;
的解析式;
(2)若函數![]() 在區間
在區間![]() 上有三個零點,求實數
上有三個零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C的方程為:ax2+ay2﹣2a2x﹣4y=0(a≠0,a為常數).
(1)判斷曲線C的形狀;
(2)設曲線C分別與x軸、y軸交于點A、B(A、B不同于原點O),試判斷△AOB的面積S是否為定值?并證明你的判斷;
(3)設直線l:y=﹣2x+4與曲線C交于不同的兩點M、N,且|OM|=|ON|,求曲線C的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),其中0<α<β<π.
=(cosβ,sinβ),其中0<α<β<π.
(1)求證: ![]() 與
與 ![]() 互相垂直;
互相垂直;
(2)若k ![]() 與
與 ![]() ﹣k
﹣k ![]() 的長度相等,求β﹣α的值(k為非零的常數).
的長度相等,求β﹣α的值(k為非零的常數).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com