【題目】已知函數f（x）= 
x3﹣4x+4，
（1）求f（x）的單調區間；
（2）求f（x）在[0，3]上的最大值和最小值．
【答案】
（1）解：因為 
，所以f'（x）=x2﹣4=（x+2）（x﹣2）…（2分）
由f'（x）＞0得x＜﹣2或x＞2，
故函數f（x）的單調遞增區間為（﹣∞，﹣2），（2，+∞）； …
由f'（x）＜0得﹣2＜x＜2
故函數f（x）的單調遞減區間為（﹣2，2）
（2）解：令f'（x）=x2﹣4=0得x=±2
由（1）可知，在[0，3]上f（x）有極小值 
，
而f（0）=4，f（3）=1，
因為 
所以f（x）在[0，3]上的最大值為4，最小值為 
．
【解析】（1）求導數，利用導數的正負，即可求f（x）的單調區間；（2）由（1）可知，在[0，3]上f（x）有極小值 
，而f（0）=4，f（3）=1，即可求f（x）在[0，3]上的最大值和最小值．
【考點精析】通過靈活運用利用導數研究函數的單調性，掌握一般的,函數的單調性與其導數的正負有如下關系： 在某個區間
內，(1)如果
，那么函數
在這個區間單調遞增；(2)如果
，那么函數
在這個區間單調遞減即可以解答此題．
陽光課堂同步練習系列答案科目：高中數學 來源： 題型：
【題目】已知函數
，(其中A＞0，ω＞0，0＜φ＜
)的圖象與x軸的交點中，相鄰兩個交點之間的距離為
，且圖象上一個最低點為M(
，－2)．
（1）求f(x)的解析式；
（2）將函數f(x)的圖象向右平移
個單位后，再將所得圖象上各點的橫坐標縮小到原來的
，縱坐標不變，得到y＝g(x)的圖象，求函數y＝g(x)的解析式．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐S—ABCD的底面為正方形，SD⊥底面ABCD，則下列結論
①AC⊥SB
②AB∥平面SCD
③SA與平面ABD所成的角等于SC與平面ABD所成的角
④AB與SC所成的角等于DC與SA所成的角．
⑤二面角
的大小為
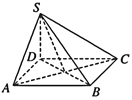
其中，正確結論的序號是________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知冪函數
，且
在
上單調遞增.
（1）求實數
的值，并寫出相應的函數
的解析式；
（2）若
在區間
上不單調，求實數
的取值范圍；
（3）試判斷是否存在正數
，使函數
在區間
上的值域為
，若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ax+ 
，其中函數f（x）的圖象在點（1，f（1））處的切線方程為y=x﹣1．
（1）若a= 
，求函數f（x）的解析式；
（2）若f（x）≥g（x）在[1，+∞）上恒成立，求實數a的取值范圍；
（3）證明：1+ 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙倆人各進行3次射擊，甲每次擊中目標的概率為 
，乙每次擊中目標的概率為 
． （Ⅰ）記甲恰好擊中目標2次的概率；
（Ⅱ）求乙至少擊中目標2次的概率；
（Ⅲ）求乙恰好比甲多擊中目標2次的概率；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某車間為了規定工時定額，需要確定加工零件所花費的時間，為此進行了5次試驗，收集數據如下：
加工零件x（個） | 10 | 20 | 30 | 40 | 50 |
加工時間y（分鐘） | 64 | 69 | 75 | 82 | 90 |
經檢驗，這組樣本數據具有線性相關關系，那么對于加工零件的個數x與加工時間y這兩個變量，下列判斷正確的是（ ）
A.成正相關，其回歸直線經過點（30，75）
B.成正相關，其回歸直線經過點（30，76）
C.成負相關，其回歸直線經過點（30，76）
D.成負相關，其回歸直線經過點（30，75）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和Sn=1﹣nan（n∈N*）
（1）計算a1 ， a2 ， a3 ， a4；
（2）猜想an的表達式，并用數學歸納法證明你的結論．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
，其中a＞0且a≠1．若a= 
時方程f（x）=b有兩個不同的實根，則實數b的取值范圍是；若f（x）的值域為[2，+∞），則實數a的取值范圍是 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com