Question

【題目】水是地球上寶貴的資源，由于價格比較便宜在很多不缺水的城市居民經常無節制的使用水資源造成嚴重的資源浪費．某市政府為了提倡低碳環保的生活理念鼓勵居民節約用水，計劃調整居民生活用水收費方案，擬確定一個合理的月用水量標準（噸），一位居民的月用水量不超過的部分按平價收費，超出的部分按議價收費．為了了解居民用水情況，通過抽樣，獲得了某年100位居民每人的月均用水量（單位：噸），將數據按照，，，…，分成9組，制成了如圖所示的頻率分布直方圖．

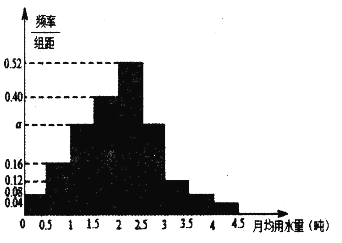
（1）若全市居民中月均用水量不低于3噸的人數為3.6萬，試估計全市有多少居民？并說明理由；

（2）若該市政府擬采取分層抽樣的方法在用水量噸數為和之間選取7戶居民作為議價水費價格聽證會的代表，并決定會后從這7戶家庭中按抽簽方式選出4戶頒發“低碳環保家庭”獎，設為用水量噸數在中的獲獎的家庭數，為用水量噸數在中的獲獎家庭數，記隨機變量，求的分布列和數學期望．

Answer 1

【答案】（1）30萬（2），分布列見解析

【解析】

試題分析：（1）根據頻率分布直方圖，求用水量大于等于3噸的頻率，頻率乘以全市的人數等于3.6萬人，求解方程；（2）首先根據頻率和為1，計算 ，再分別計算用水量在 和 的戶數，再根據分層抽樣計算兩組分別抽取多少戶，再列舉所有 的情況，以及隨機變量的值，最后得到的分布列和數學期望.

試題解析：（1）由圖，不低于3噸人數所占百分比為，所以假設全市的人數為（萬人），則有，解得，

所以估計全市人數為30萬．

（2）由概率統計相關知識，各組頻率之和的值為1，

因為頻率，

所以，得，

用水量在之間的戶數為戶，而用水量在噸之間的戶數為戶，根據分層抽樣的方法，總共需要抽取7戶居民，所以用水量在之間應抽取的戶數為戶，而用水量在噸之間的戶數為戶．

據題意可知隨機變量的取值為0,2,4．

，

，

，

其分布列為：

	0	2	4

期望為：．