【題目】（12分）
一只藥用昆蟲的產卵數y（單位：個）與一定范圍內的溫度
（單位：℃）有關，現收集了該種藥用昆蟲的6組觀測數據如下表所示.
經計算得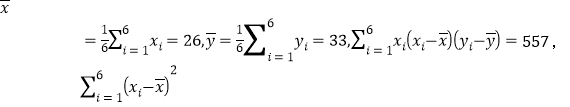
，線性回歸模型的殘差平方和
，其中
分別為觀測數據中的溫度和產卵數，
（1）若用線性回歸模型，求
的回歸方程
（結果精確到0.1）.
（2）若用非線性回歸模型預測當溫度為35℃時，該種藥用昆蟲的產卵數（結果取整數）.
附：一組數據
，其回歸直線的斜率和截距的最小二乘估計分別為
.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別是
，其離心率
，點
為橢圓上的一個動點，
面積的最大值為3.
（1）求橢圓
的標準方程；
（2）已知點
，過點
且斜率不為0的直線
與橢圓相交于
兩點，直線
，
與
軸分別相交于
兩點，試問
是否為定值？如果，求出這個定值；如果不是，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（12分）
如圖，在四棱錐
.
（1）當PB=2時，證明：平面
平面ABCD.
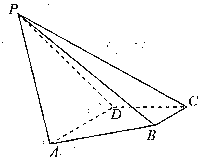（2）當四棱錐
的體積為
，且二面角
為鈍角時，求直線PA與平面PCD所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了調查某社區居民每天參加健身的時間，某機構在該社區隨機采訪男性、女性各50名，其中每人每天的健身時間不少于1小時稱為“健身族”，否則稱其為"非健身族”，調查結果如下：
健身族 | 非健身族 | 合計 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合計 | 70 | 30 | 100 |
（1）若居民每人每天的平均健身時間不低于70分鐘，則稱該社區為“健身社區”. 已知被隨機采訪的男性健身族，男性非健身族，女性健身族，女性非健身族每人每天的平均健分時間分別是1.2小時，0.8小時，1.5小時，0.7小時，試估計該社區可否稱為“健身社區”？
（2）根據以上數據，能否在犯錯誤的概率不超過5%的情況下認為“健身族”與“性別”有關？
參考公式：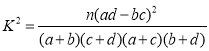 
，其中
.
參考數據：
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4-4：坐標系與參數方程]（10分）
在極坐標系中，圓C的極坐標方程為
，若以極點O為原點，極軸為x軸的正半軸建立平面直角坐標系.
（1）求圓C的一個參數方程；
（2）在平面直角坐標系中，
是圓C上的動點，試求
的最大值，并求出此時點P的直角坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某社區組織“學習強國”的知識競賽，從參加競賽的市民中抽出40人，將其成績分成以下6組：第1組
，第2組
，第3組
，第4組
，第5組
，第6組
，得到如圖所示的頻率分布直方圖．現采用分層抽樣的方法，從第2，3，4組中按分層抽樣抽取8人，則第2，3，4組抽取的人數依次為（ ）
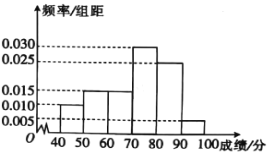
A.1，3，4B.2，3，3C.2，2，4D.1，1，6
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，已知AB＝a，BC＝b(a>b)，在AB，AD，CB，CD上，分別截取AE＝AH＝CF＝CG＝x(x>0)，設四邊形EFGH的面積為y.
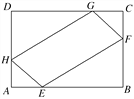
(1)寫出四邊形EFGH的面積y與x之間的函數關系；
(2)求當x為何值時y取得最大值，最大值是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
