
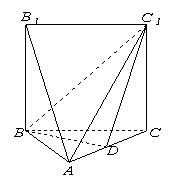
如圖,五面體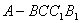 中,
中,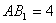 .底面
.底面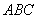 是正三角形,
是正三角形,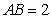 .四邊形
.四邊形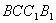 是矩形,二面角
是矩形,二面角 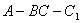 為直二面角.
為直二面角.
(1)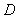 在
在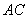 上運動,當
上運動,當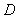 在何處時,有
在何處時,有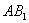 ∥平面
∥平面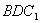 ,并且說明理由;
,并且說明理由;
(2)當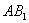 ∥平面
∥平面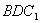 時,求二面角
時,求二面角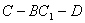 的余弦值.
的余弦值.
解: (Ⅰ)當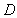 為
為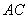 中點時,有
中點時,有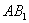 ∥平面
∥平面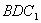 .…1分
.…1分
 證明:連結
證明:連結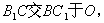 連結
連結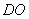 ,
,
∵四邊形 是矩形 ∴
是矩形 ∴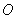 為
為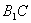 中點
中點
∵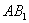 ∥平面
∥平面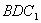 ,
,
且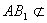 平面
平面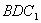 ,
,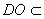 平面
平面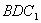
∴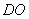 ∥
∥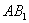 ,------------------5分
,------------------5分
∴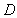 為
為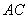 的中點.------------------6分
的中點.------------------6分
(Ⅱ)建立空間直角坐標系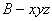 如圖所示,
如圖所示,
則 ,
, ,
, ,
,

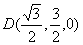 ,
, ------------8分
------------8分
所以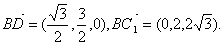
設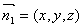 為平面
為平面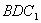 的法向量,
的法向量,
則有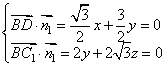 ,
,
即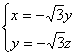
令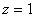 ,可得平面
,可得平面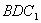 的一個
的一個
法向量為 , ----------------11分
, ----------------11分
而平面 的法向量為
的法向量為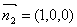 , ---------------------------12分
, ---------------------------12分
所以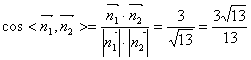 ,
,
所以二面角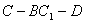 的余弦值為
的余弦值為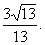 ----------------------------14分
----------------------------14分


科目:高中數學 來源: 題型:
(本題14![]() 分)如圖,五面體
分)如圖,五面體![]()
![]() 中
中![]()
![]() ,
,![]() .底面
.底面![]() 是正三角形,
是正三角形,![]() .
.![]() 四邊形
四邊形![]() 是矩形
是矩形![]() ,
,![]() 二面角
二面角![]()
![]() 為直二面角.
為直二面角.
(1)![]() 在
在![]()
![]() 上運動,當
上運動,當![]() 在何處時,有
在何處時,有![]() ∥平面
∥平面![]() ,并且
,并且![]() 說明理由;
說明理由;
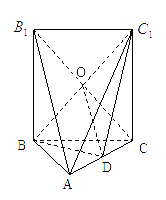
![]()
![]() (2)當
(2)當![]() ∥平面
∥平面![]() 時,求二面角
時,求二面角![]()
![]() 的
的![]() 余弦值.
余弦值.
查看答案和解析>>
科目:高中數學 來源:2011屆吉林省普通中學高中畢業班下學期期中考試數學理卷 題型:解答題
(本小題滿分12分)
如圖,五面體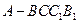 中,
中,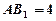 .底面
.底面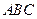 是正三角形,
是正三角形,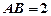 .四邊形
.四邊形 是矩形,二面角
是矩形,二面角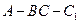 為直二面角.
為直二面角.
(Ⅰ) 在
在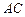 上運動,當
上運動,當 在何處時,有
在何處時,有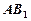 ∥平面
∥平面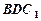 ,
,
并且說明理由;
(Ⅱ)當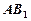 ∥平面
∥平面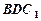 時,求二面角
時,求二面角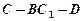 余弦值.
余弦值.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年吉林省高中畢業班下學期期中考試數學理卷 題型:解答題
(本小題滿分12分)
如圖,五面體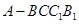 中,
中,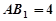 .底面
.底面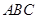 是正三角形,
是正三角形,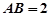 .四邊形
.四邊形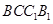 是矩形,二面角
是矩形,二面角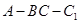 為直二面角.
為直二面角.

(Ⅰ)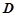 在
在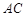 上運動,當
上運動,當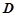 在何處時,有
在何處時,有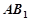 ∥平面
∥平面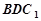 ,
,
并且說明理由;
(Ⅱ)當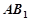 ∥平面
∥平面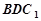 時,求二面角
時,求二面角 余弦值.
余弦值.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年吉林省吉林市高三下學期期中考試數學理卷 題型:解答題
(本小題滿分12分)
如圖,五面體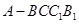 中,
中,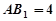 .底面
.底面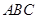 是正三角
是正三角
形, .四邊形
.四邊形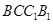 是矩形,二面角
是矩形,二面角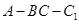 為
為
直二面角.
(Ⅰ)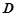 在
在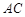 上運動,當
上運動,當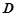 在何處時,有
在何處時,有 ∥平面
∥平面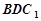 ,
,
并且說明理由;
(Ⅱ)當 ∥平面
∥平面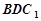 時,求二面角
時,求二面角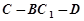 余弦值.
余弦值.

查看答案和解析>>
科目:高中數學 來源:安徽省宿州市2010屆高三第三次教學質檢(理) 題型:解答題
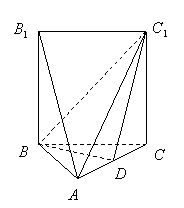 如圖,五面體
如圖,五面體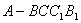 中,
中,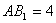 .底面
.底面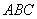 是正三角形,
是正三角形,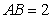 .四邊形
.四邊形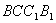 是矩形,平面
是矩形,平面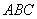
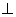 平面
平面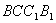
(I)求這個幾何體的體積;
(Ⅱ)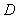 在
在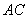 上運動,問:當
上運動,問:當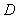 在何處時,有
在何處時,有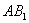 ∥平面
∥平面 ,請說明理由;
,請說明理由;
(III)求二面角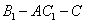 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com