【題目】某家電公司銷售部門共有200位銷售員，每位部門對每位銷售員都有1400萬元的年度銷售任務，已知這200位銷售員去年完成銷售額都在區間
（單位：百萬元）內，現將其分成5組，第1組，第2組，第3組，第4組，第5組對應的區間分別為
， 
， 
， 
， 
，繪制出頻率分布直方圖.
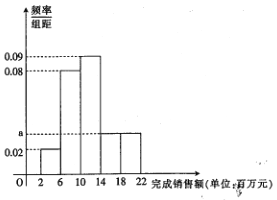
（1）求
的值，并計算完成年度任務的人數；
（2）用分層抽樣從這200位銷售員中抽取容量為25的樣本，求這5組分別應抽取的人數；
（3）現從（2）中完成年度任務的銷售員中隨機選取2位，獎勵海南三亞三日游，求獲得此獎勵的2位銷售員在同一組的概率.
【答案】（Ⅰ）
,
;（Ⅱ）見解析; （Ⅲ）
．
【解析】試題分析：（1）頻率分布直方圖中所有小長方形面積之和為1,所以有
，解得
的值，根據小長方形面積對應區間概率,以及頻數等于總數與頻率乘積得完成年度任務的人數為
.（2）分成抽樣就是按比例,可按小長方形縱坐標之比進行分人數,（3）完成年度任務的銷售員中共有6人,利用枚舉法得6人中隨機選取2位，所有的基本事件數為15,其中在同一組基本事件數有6個，最后根據古典概型概率公式計算概率.
試題解析：（Ⅰ）∵
，∴
．
完成年度任務的人數為
.
（Ⅱ）第1組應抽取的人數為
，
第2組應抽取的人數為
，
第3組應抽取的人數為
，
第4組應抽取的人數為
，
第5組應抽取的人數為
．
（Ⅲ）在（Ⅱ）中完成年度任務的銷售員中，第4組有3人，記這3人分別為
， 
， 
，第5組有3人，記這3人分別為
， 
， 
．
從這6人中隨機選取2位，所有的基本事件為： 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
，共有15個基本事件．
獲得此獎勵的2位銷售員在同一組的基本事件有6個，
故所求概率為
．
科目：高中數學 來源： 題型：
【題目】某出租車公司響應國家節能減排的號召，已陸續購買了140輛純電動汽車作為運營車輛，目前我國主流純電動汽車按續航里程數
．（單位：公里）分為3類，即
類：
，
類：
， 
類：
，該公司對這140輛車的行駛總里程進行統計，結果如下表：
類型 |
|
|
|
已行駛總里程不超過10萬公里的車輛數 | 10 | 40 | 30 |
已行駛總里程超過10萬公里的車輛數 | 20 | 20 | 20 |
（1）從這140輛汽車中任取一輛，求該車行駛總里程超過10萬公里的概率；
（2）公司為了了解這些車的工作狀況，決定抽取了14輛車進行車況分析，按表中描述的六種情況進行分層抽樣，設從
類車中抽取了
輛車．
①求
的值；
②如果從這
輛車中隨機選取兩輛車，求恰有一輛車行駛總里程超過10萬公里的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若要得到函數y=sin（2x﹣ 
）的圖象，可以把函數y=sin2x的圖象（ ）
A.向右平移 
個單位
B.向左平移 個單位
C.向右平移 個單位
D.向左平移 個單位
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（2cosωx，cos2ωx）， 
=（sinωx，1）（其中ω＞0），令f（x）= 
，且f（x）的最小正周期為π．
（1）求 
的值；
（2）寫出 
上的單調遞增區間．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的右焦點為
，離心率為
，設直線
的斜率是
，且
與橢圓
交于
， 
兩點.
（Ⅰ）求橢圓的標準方程.
（Ⅱ）若直線
在
軸上的截距是
，求實數
的取值范圍.
（Ⅲ）以
為底作等腰三角形，頂點為
，求
的面積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】記Sn為正項等比數列{an}的前n項和，若 
﹣7 
﹣8=0，且正整數m，n滿足a1ama2n=2 
，則 
+ 
的最小值是（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
