
���}Ŀ����֪���タ![]() ��
�� ![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ����(zh��n)����
����(zh��n)����![]() �������c(di��n)
�������c(di��n)![]() ��
�� ![]() ��
�� ![]() ��ǡ�Ѓɂ��c(di��n)��
��ǡ�Ѓɂ��c(di��n)��![]() �ϣ�
�ϣ�
��1�����タ![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2���^![]() ��ֱ����
��ֱ����![]() ��
��![]() ��
�� ![]() ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)![]() ��
��![]() ������һ�c(di��n)���C����ֱ��
������һ�c(di��n)���C����ֱ��![]() ��
�� ![]() ��
�� ![]() ��б�ʳɵȲ(sh��)�У�
��б�ʳɵȲ(sh��)�У�
���𰸡�(1) ![]() (2)Ҋ����
(2)Ҋ����
��������ԇ�}��������1���Ɍ��Q�P(gu��n)ϵ��֪�� ![]() ���c(di��n)��
���c(di��n)��![]() �ϣ���Ò��タ
�ϣ���Ò��タ![]() �Ę�(bi��o)��(zh��n)���̞�
�Ę�(bi��o)��(zh��n)���̞�![]() ����2���O(sh��)ֱ��
����2���O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��(li��n)�����タ���̣��õ��f�_(d��)����
��(li��n)�����タ���̣��õ��f�_(d��)����![]() ����ʾ��ֱ��
����ʾ��ֱ��![]() ��б��
��б��![]() ���C���M��Ȳ����(xi��ng)��ʽ���ɡ�
���C���M��Ȳ����(xi��ng)��ʽ���ɡ�
ԇ�}������
��I����?y��n)钁�タ![]() ��
�� ![]() �P(gu��n)��x�S���Q��
�P(gu��n)��x�S���Q��
����![]() ��ֻ����
��ֻ����![]() ���c(di��n)��
���c(di��n)��![]() �ϣ�
�ϣ�
��������(bi��o)��![]() �����Ԓ��タ
�����Ԓ��タ![]() �Ę�(bi��o)��(zh��n)���̞�
�Ę�(bi��o)��(zh��n)���̞�![]()
��II���C�������タ�Ľ��c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ����(zh��n)��
����(zh��n)��![]() �ķ��̞�
�ķ��̞�![]() .
.
�O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
�� ![]() .
.
��![]() ���ɵ�
���ɵ�![]() ������
������![]() ��
��
����![]() ��
�� ![]()
�O(sh��)ֱ��![]() ��б�ʷքe��
��б�ʷքe��![]() ��
��
һ���棬 ![]()
![]()
![]()
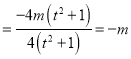 .
.
��һ���棬 ![]() .
.
����![]() ����ֱ��
����ֱ��![]() ��б�ʳɵȲ(sh��)��
��б�ʳɵȲ(sh��)��


 ��У�n��ϵ�д�
��У�n��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���錦�Ͽ��^(q��)���ڶ��h�Ʌ^(q��)�hij��(li��n)���ɿ��M(j��n)�з������S�C(j��)����˃ɵ�һ��10000�������ijɿ�������(j��)���Ô�(sh��)��(j��)�������µĘӱ��l�ʷֲ�ֱ���D��

(1)��ɿ���![]() ���l�ʣ�
���l�ʣ�
(2)����(j��)�l�ʷֲ�ֱ���D����ӱ���(sh��)��(j��)ƽ����(sh��)��
(3)���˷����ɿ��c�༉���W(xu��)У�ȷ�����P(gu��n)ϵ����횰��ɿ��ُ��@10000�����÷ӳ�ӷ������20�����M(j��n)һ���������t�ɿ���![]() ���@�Α�(y��ng)������ˣ�
���@�Α�(y��ng)������ˣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����˽�ij�^(q��)ij�N�r(n��ng)�a(ch��n)Ʒ����a(ch��n)��![]() ����λ���������r��
����λ���������r��![]() ����λ��ǧԪ/����������
����λ��ǧԪ/����������![]() ��Ӱ푣���������ԓ�r(n��ng)�a(ch��n)Ʒ����a(ch��n)���̓r��y(t��ng)Ӌ���±���
��Ӱ푣���������ԓ�r(n��ng)�a(ch��n)Ʒ����a(ch��n)���̓r��y(t��ng)Ӌ���±���
| 1 | 2 | 3 | 4 | 5 |
| 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
��֪![]() ��
��![]() ���о������P(gu��n)�P(gu��n)ϵ.
���о������P(gu��n)�P(gu��n)ϵ.
������![]() �P(gu��n)��
�P(gu��n)��![]() �ľ��Իؚw����
�ľ��Իؚw����![]() ��
��
������ÿ��ԓ�r(n��ng)�a(ch��n)Ʒ�ijɱ���2ǧԪ�����O(sh��)ԓ�r(n��ng)�a(ch��n)Ʒ��ȫ���u�����A(y��)�y��(d��ng)��a(ch��n)������ه��r��������![]() ȡ�����ֵ��������һλС��(sh��)��
ȡ�����ֵ��������һλС��(sh��)��
������(sh��)��(j��)����ʽ�� ![]() ��
�� ![]() ��
��

 ��
�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���ڎ��w�У���߅��![]() �����Σ����Ǿ�
�����Σ����Ǿ�![]() �c
�c![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ����߅��
����߅��![]() �����Σ�
������ ![]() .
.
������![]() �����C��
�����C�� ![]() ƽ��
ƽ��![]() ��
��
�������C��ƽ��![]() ƽ��
ƽ��![]() ��
��
������![]() ��
�� ![]() ��
�� ![]() ����
����![]() �cƽ��
�cƽ��![]() ���ɽ�.
���ɽ�.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1��ӑՓ����(sh��)![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��2����(d��ng)![]() �r��ӛ����(sh��)
�r��ӛ����(sh��)![]() �ĘOСֵ��
�ĘOСֵ��![]() ����
����![]() ���������M��l����������(sh��)
���������M��l����������(sh��)![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ�У� ![]() �ăɂ���c(di��n)
�ăɂ���c(di��n)![]() ������(bi��o)�քe��
������(bi��o)�քe��![]() ��������(n��i)��
��������(n��i)��![]() �M��
�M��![]() .
.
��1������c(di��n)![]() ��܉�E��
��܉�E��![]() ��������
��������![]() �ķ��̣�
�ķ��̣�
��2�����c(di��n)![]() ������
������![]() �ϵ�һ�c(di��n)���^�c(di��n)
�ϵ�һ�c(di��n)���^�c(di��n)![]() ������
������![]() ������A
���о����A![]() �ڲ�ͬ�ă��c(di��n)
�ڲ�ͬ�ă��c(di��n)![]() ������
������![]() ��
��![]() ���҂�(c��)��������߅��
���҂�(c��)��������߅��![]() ��e�����ֵ.
��e�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)�E�A![]() ���x���ʞ�
���x���ʞ�![]() �����^�c(di��n)
�����^�c(di��n)![]() .
.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���Ƿ���ڈA����ԭ�c(di��n)�ĈA��ʹ��ԓ�A������һ�l�о��c�E�A![]() ���Ѓɂ����c(di��n)
���Ѓɂ����c(di��n)![]() �� ��
�� ��![]() ��
��![]() ������(bi��o)ԭ�c(di��n)���������ڣ�����ԓ�A�ķ��̣��������ڣ��f������.
������(bi��o)ԭ�c(di��n)���������ڣ�����ԓ�A�ķ��̣��������ڣ��f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�P(gu��n)��![]() ��һԪ���η���
��һԪ���η���![]() ������
������![]() ��
��
��I����![]() �S�C(j��)�x�Լ���
�S�C(j��)�x�Լ���![]() ��
��![]() �S�C(j��)�x�Լ���
�S�C(j��)�x�Լ���![]() �����Ќ�(sh��)���ĸ���;
�����Ќ�(sh��)���ĸ���;
��������![]() �S�C(j��)�x�ԅ^(q��)�g
�S�C(j��)�x�ԅ^(q��)�g![]() ��
��![]() �S�C(j��)�x�ԅ^(q��)�g
�S�C(j��)�x�ԅ^(q��)�g![]() �����Ќ�(sh��)���ĸ��ʡ�
�����Ќ�(sh��)���ĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
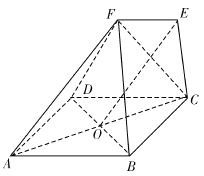
���}Ŀ����֪AF![]() ƽ��ABCD����߅��ABEF����Σ���߅��ABCD��ֱ�����Σ�
ƽ��ABCD����߅��ABEF����Σ���߅��ABCD��ֱ�����Σ� ![]() .
.
��1�����C�� ![]() ƽ��
ƽ��![]() ��
��
��2������![]() ���Ƿ����һ�c(di��n)
���Ƿ����һ�c(di��n)![]() ��ʹ��
��ʹ��![]() ?�����ڣ��_���c(di��n)
?�����ڣ��_���c(di��n)![]() ��λ�ã��������ڣ�Ո�f�����ɣ�
��λ�ã��������ڣ�Ո�f�����ɣ�
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com