【題目】已知函數
， 
，函數
的圖象在點
處的切線平行于
軸.
(1)求
的值；
(2)求函數
的極小值；
(3)設斜率為
的直線與函數
的圖象交于兩點
， 
， 
，證明： 
.
【答案】(1) 
(2) 函數
的極小值為
.(3) 見解析
【解析】試題分析：（1）由導數幾何意義得
，解得
.（2）先求導函數零點，列表分析導函數符號變化規律，進而確定極小值點（3）先利用斜率公式化簡所證不等式
，再利用換元
轉化為
，最后根據導數分別證明
及
試題解析：解：(1)依題意得
，則
.
由函數
的圖象在點
處的切線平行于
軸得：
，所以
.
(2)由(1)得
，
因為函數
的定義域為
，令
得
或
.
函數
在
上單調遞增，在
上單調遞減；在
上單調遞增，
故函數
的極小值為
.
(3)證法一：依題意得
，
要證
，即證
，
因
，即證
，
令
，即證
，
令
，則
，所以
在
上單調遞減，
所以
，即
，所以
①
令
，則
，
所以
在
上單調遞增，
所以
，即
②
綜①②得
，即
.
證法二：依題意得
，
令
，則
，
由
得
，當
時， 
，當
時， 
，
所以
在
單調遞增，在
單調遞減，又
，
所以
，即
.
文敬圖書課時先鋒系列答案科目：高中數學 來源： 題型：
【題目】某廠生產
和
兩種產品，按計劃每天生產
各不得少于10噸，已知生產
產品
噸需要用煤9噸，電4度，勞動力3個(按工作日計算).生產
產品1噸需要用煤4噸，電5度，勞動力10個，如果
產品每噸價值7萬元， 
產品每噸價值12萬元，而且每天用煤不超過300噸，用電不超過200度，勞動力最多只有300個，每天應安排生產
兩種產品各多少才是合理的？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】記全集U={1，2，3，4，5，6，7，8}，A={1，2，3，5}，B={2，4，6}，則圖中陰影部分所表示的集合是（ ）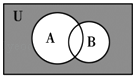 
A.{4，6，7，8}
B.{2}
C.{7，8}
D.{1，2，3，4，5，6}
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數g（x）=log2x，x∈（0，2），若關于x的方程|g（x）|2+m|g（x）|+2m+3=0有三個不同實數解，則實數m的取值范圍為 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
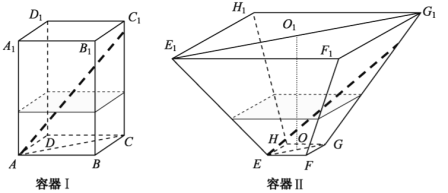
【題目】如圖，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱臺形玻璃容器Ⅱ的高均為32cm，容器Ⅰ的底面對角線AC的長為10
cm，容器Ⅱ的兩底面對角線
，
的長分別為14cm和62cm．分別在容器Ⅰ和容器Ⅱ中注入水，水深均為12cm．現有一根玻璃棒l，其長度為40cm．（容器厚度、玻璃棒粗細均忽略不計）
（1）將
放在容器Ⅰ中，的一端置于點A處，另一端置于側棱
上，求沒入水中部分的長度；
（2）將放在容器Ⅱ中，的一端置于點E處，另一端置于側棱
上，求沒入水中部分的長度．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定義在R上的偶函數f（x），當x≥0時，f（x）=x2﹣4x
（1）求f（﹣2）的值；
（2）當x＜0時，求f（x）的解析式；
（3）設函數f（x）在[t﹣1，t+1]（t＞1）上的最大值為g（t），求g（t）的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
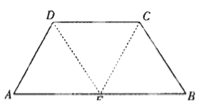
【題目】【2017開封高三模擬理】如圖，在等腰梯形ABCD中，AB＝2DC＝2，∠DAB＝60°，E為AB的中點．將△ADE與△BEC分別沿ED、EC向上折起，使A、B重合于點P，則三棱錐P-DCE的外接球的體積為( )
A．
B．
C．
D．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
