
【題目】某校100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區間是:[50,60),[60,70),[70,80),[80,90),[90,100]. 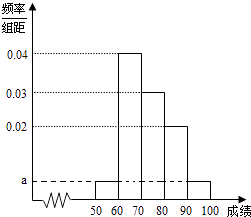
(1)求圖中a的值;
(2)根據頻率分布直方圖,估計這100名學生語文成績的平均分;
(3)若這100名學生語文成績某些分數段的人數(x)與數學成績相應分數段的人數(y)之比如表所示,求數學成績在[50,90)之外的人數.
分數段 | [50,60) | [60,70) | [70,80) | [80,90) |
x:y | 1:1 | 2:1 | 3:4 | 4:5 |
【答案】
(1)解:依題意得,10(2a+0.02+0.03+0.04)=1,解得a=0.005
(2)解:這100名學生語文成績的平均分為:55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73(分)
(3)解:數學成績在[50,60)的人數為:100×0.05=5,
數學成績在[60,70)的人數為: ![]() ,
,
數學成績在[70,80)的人數為: ![]() ,
,
數學成績在[80,90)的人數為: ![]() ,
,
所以數學成績在[50,90)之外的人數為:100﹣5﹣20﹣40﹣25=10
【解析】(1)由頻率分布直方圖的性質可10(2a+0.02+0.03+0.04)=1,解方程即可得到a的值;(2)由平均數加權公式可得平均數為55×0.05+65×0.4+75×0.3+85×0.2+95×0.05,計算出結果即得;(3)按表中所給的數據分別計算出數學成績在分數段的人數,從總人數中減去這些段內的人數即可得出數學成績在[50,90)之外的人數.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知曲線![]() ,
, ![]() ,則下列說法正確的是( )
,則下列說法正確的是( )
A. 把![]() 上各點橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移
上各點橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]()
B. 把![]() 上各點橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移
上各點橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]()
C. 把曲線![]() 向右平移
向右平移![]() 個單位長度,再把得到的曲線上各點橫坐標縮短到原來的
個單位長度,再把得到的曲線上各點橫坐標縮短到原來的![]() ,縱坐標不變,得到曲線
,縱坐標不變,得到曲線![]()
D. 把曲線![]() 向右平移
向右平移![]() 個單位長度,再把得到的曲線上各點橫坐標縮短到原來的
個單位長度,再把得到的曲線上各點橫坐標縮短到原來的![]() ,縱坐標不變,得到曲線
,縱坐標不變,得到曲線![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設向量 ![]() =(cosθ,sinθ),
=(cosθ,sinθ), ![]() =(﹣
=(﹣ ![]() ,
, ![]() );
);
(1)若 ![]() ∥
∥ ![]() ,且θ∈(0,π),求θ;
,且θ∈(0,π),求θ;
(2)若|3 ![]() +
+ ![]() |=|
|=| ![]() ﹣3
﹣3 ![]() |,求|
|,求| ![]() +
+ ![]() |的值.
|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家庭進行理財投資,根據長期收益率市場調查和預測,投資債券等穩鍵型產品A的收益與投資成正比,其關系如圖1所示;投資股票等風險型產品B的收益與投資的算術平方根成正比,其關系如圖2所示(收益與投資單位:萬元). 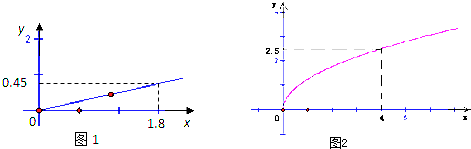
(1)分別將A、B兩種產品的收益表示為投資的函數關系式;
(2)該家庭現有10萬元資金,并全部投資債券等穩鍵型產品A及股票等風險型產品B兩種產品,問:怎樣分配這10萬元投資,才能使投資獲得最大收益,其最大收益為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 且a1=2,an+1= ![]() Sn(n=1,2,3,…).
Sn(n=1,2,3,…).
(1)證明:數列{ ![]() }是等比數列;
}是等比數列;
(2)設bn= ![]() ,求數列{bn}的前n項和Tn .
,求數列{bn}的前n項和Tn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com