
【題目】某分公司經銷某種品牌產品,每件產品的成本為30元,并且每件產品須向總公司繳納a元(a為常數,2≤a≤5)的管理費,根據多年的統計經驗,預計當每件產品的售價為x元時,產品一年的銷售量為 ![]() (e為自然對數的底數)萬件,已知每件產品的售價為40元時,該產品一年的銷售量為500萬件.經物價部門核定每件產品的售價x最低不低于35元,最高不超過41元.
(e為自然對數的底數)萬件,已知每件產品的售價為40元時,該產品一年的銷售量為500萬件.經物價部門核定每件產品的售價x最低不低于35元,最高不超過41元.
(1)求分公司經營該產品一年的利潤L(x)萬元與每件產品的售價x元的函數關系式;
(2)當每件產品的售價為多少元時,該產品一年的利潤L(x)最大,并求出L(x)的最大值.
【答案】
(1)解:由題意,該產品一年的銷售量為y= ![]() .
.
將x=40,y=500代入,得k=500e40.
故該產品一年的銷售量y(萬件)關于x(元)的函數關系式為y=500e40-x.
所以L(x)=(x-30-a)y=500(x-30-a)e40-x(35≤x≤41).
(2)解:由(1)得,L′(x)=500[e40-x-(x-30-a)e40-x]=500e40-x(31+a-x).
①當2≤a≤4時,L′(x)≤500e40-x(31+4-35)=0,
當且僅當a=4,x=35時取等號.
所以L(x)在[35,41]上單調遞減.
因此,L(x)max=L(35)=500(5-a)e5.
②當4<a≤5時,L′(x)>035≤x<31+a,
L′(x)<031+a<x≤41.
所以L(x)在[35,31+a)上單調遞增,在[31+a,41]上單調遞減.
因此,L(x)max=L(31+a)=500e9-a.
綜上所述當2≤a≤4時,每件產品的售價為35元,該產品一年的利潤L(x)最大,最大為500(5-a)e5萬元;
當4<a≤5時,每件產品的售價為(31+a)元時,該產品一年的利潤L(x)最大,最大為500e9-a萬元.
【解析】(1)由每件產品的售價為40元時,該產品一年的銷售量為500萬件,代入可得k值,進而根據利潤=單件利潤×銷售量得到該產品一年的利潤L(x)萬元與每件產品的售價x元的函數關系式;
(2)由(1)中所得函數的解析式,求導后分析函數的單調性,進而分析出該產品一年的利潤L(x)的最大值.


科目:高中數學 來源: 題型:
【題目】在極坐標系下,知圓O:ρ=cosθ+sinθ和直線 ![]() .
.
(1)求圓O與直線l的直角坐標方程;
(2)當θ∈(0,π)時,求圓O和直線l的公共點的極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體 ![]() 的棱長為1,
的棱長為1, ![]() 分別是棱
分別是棱 ![]() 的中點,過
的中點,過 ![]() 的平面與棱
的平面與棱 ![]() 分別交于點
分別交于點 ![]() .設
.設 ![]() ,
, ![]() .
.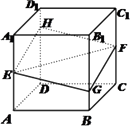
①四邊形 ![]() 一定是菱形;②
一定是菱形;② ![]() 平面
平面 ![]() ;③四邊形
;③四邊形 ![]() 的面積
的面積 ![]() 在區間
在區間 ![]() 上具有單調性;④四棱錐
上具有單調性;④四棱錐 ![]() 的體積為定值.
的體積為定值.
以上結論正確的個數是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)=2x2-ln x在其定義域內的一個子區間(k-1,k+1)內不是單調函數,則實數k的取值范圍是( )
A.[1,+∞)
B.[1,2)
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線 ![]() 的焦點為
的焦點為 ![]() ,準線為
,準線為 ![]() ,點
,點 ![]() 在拋物線
在拋物線 ![]() 上,已知以點
上,已知以點 ![]() 為圓心,
為圓心, ![]() 為半徑的圓
為半徑的圓 ![]() 交
交 ![]() 于
于 ![]() 兩點.
兩點.
(Ⅰ)若 ![]() ,
, ![]() 的面積為4,求拋物線
的面積為4,求拋物線 ![]() 的方程;
的方程;
(Ⅱ)若 ![]() 三點在同一條直線
三點在同一條直線 ![]() 上,直線
上,直線 ![]() 與
與 ![]() 平行,且
平行,且 ![]() 與拋物線
與拋物線 ![]() 只有一個公共點,求直線
只有一個公共點,求直線 ![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com