
【題目】已知函數![]() ,
,![]() .
.
(1)若![]() 在
在![]() 處取得極值,求
處取得極值,求![]() 的值;
的值;
(2)設![]() ,試討論函數
,試討論函數![]() 的單調性;
的單調性;
(3)當![]() 時,若存在正實數
時,若存在正實數![]() 滿足
滿足![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() .
.
(2)見解析.
(3)證明見解析.
【解析】
(1)先求導![]() ,再令
,再令![]() 即得a的值,再驗證.(2)先求導得
即得a的值,再驗證.(2)先求導得![]() ,再對a分類討論得函數
,再對a分類討論得函數![]() 的單調性.(3)先化簡已知得到
的單調性.(3)先化簡已知得到![]() ,再令
,再令![]() ,
,![]() ,求得
,求得![]()
的最小值為1,解不等式![]() 即得
即得![]() .
.
(1)解:因為![]() ,所以
,所以![]() ,
,
因為![]() 在
在![]() 處取得極值,
處取得極值,
所以![]() ,解得
,解得![]() .
.
驗證:當![]() 時,
時,![]() ,
,
易得![]() 在
在![]() 處取得極大值.
處取得極大值.
(2)解:因為![]() ,
,
所以![]() .
.
①若![]() ,則當
,則當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() ,
,![]() 函數
函數![]() 在
在![]() 上單調遞減.
上單調遞減.
②若![]() ,
,![]() ,
,
當![]() 時,易得函數
時,易得函數![]() 在
在![]() 和
和![]() 上單調遞增,
上單調遞增,
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時,![]() 恒成立,所以函數
恒成立,所以函數![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,易得函數
時,易得函數![]() 在
在![]() 和
和![]() 上單調遞增,
上單調遞增,
在![]() 上單調遞減.
上單調遞減.
(3)證明:當![]() 時,
時,![]() ,
,
因為![]() ,
,
所以![]() ,
,
即![]() ,
,
所以![]() .
.
令![]() ,
,![]() ,
,
則![]() ,
,
當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞增.
上單調遞增.
所以函數![]() 在
在![]() 時,取得最小值,最小值為
時,取得最小值,最小值為![]() .
.
所以![]() ,
,
即![]() ,所以
,所以![]() 或
或![]() .
.
因為![]() 為正實數,所以
為正實數,所以![]() .
.
當![]() 時,
時,![]() ,此時不存在
,此時不存在![]() 滿足條件,
滿足條件,
所以![]() .
.


科目:高中數學 來源: 題型:
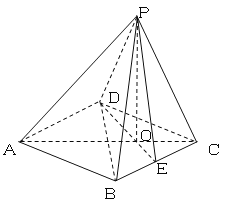
【題目】如圖,已知四棱錐P-ABCD的底面是邊長為2的菱形,∠BCD=60°,點E是BC邊
的中點,AC,DE交于點O,![]() ,且PO⊥平面ABCD.
,且PO⊥平面ABCD.
(1)求證:PD⊥BC;
(2)在線段AP上找一點F,使得BF∥平面PDE,并求此時四面體PDEF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 數列
數列![]() 的前
的前![]() 項和,對任意
項和,對任意![]() ,都有
,都有![]() (
(![]() 為常數).
為常數).
(1)當![]() 時,求
時,求![]() ;
;
(2)當![]() 時,
時,
(ⅰ)求證:數列![]() 是等差數列;
是等差數列;
(ⅱ)若對任意![]() ,必存在
,必存在![]() 使得
使得![]() ,已知
,已知![]() ,且
,且![]() ,求數列
,求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】因市場戰略儲備的需要,某公司![]() 月
月![]() 日起,每月
日起,每月![]() 日購買了相同金額的某種物資,連續購買了
日購買了相同金額的某種物資,連續購買了![]() 次.由于市場變化,
次.由于市場變化,![]() 月
月![]() 日該公司不得不將此物資全部賣出.已知該物資的購買和賣出都是以份為計價單位進行交易,且該公司在買賣的過程中沒有虧本,那么下面
日該公司不得不將此物資全部賣出.已知該物資的購買和賣出都是以份為計價單位進行交易,且該公司在買賣的過程中沒有虧本,那么下面![]() 個折線圖中,所有可以反映這種物資每份價格(單位:萬元)的變化情況的是( )
個折線圖中,所有可以反映這種物資每份價格(單位:萬元)的變化情況的是( )

A.①②B.①③C.②③D.③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC-A1B1C1中,AA1![]() AB
AB![]() AC
AC![]() 2,AB⊥AC,M是棱BC的中點點P在線段A1B上.
2,AB⊥AC,M是棱BC的中點點P在線段A1B上.
(1)若P是線段A1B的中點,求直線MP與直線AC所成角的大小;
(2)若![]() 是
是![]() 的中點,直線
的中點,直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求線段BP的長度.
,求線段BP的長度.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 同時滿足:⑴對于定義域上的任意
同時滿足:⑴對于定義域上的任意![]() ,恒有
,恒有![]() ; ⑵對于定義域上的任意
; ⑵對于定義域上的任意![]() ,當
,當![]() 時,恒有
時,恒有![]() ,則稱函數
,則稱函數![]() 為“理想函數”.給出下列四個函數中: ①
為“理想函數”.給出下列四個函數中: ①![]() ,②
,②![]() , ③
, ③![]() ,④
,④ ,能被稱為“理想函數”的有_____________(填相應的序號).
,能被稱為“理想函數”的有_____________(填相應的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,
中,![]() ,底面
,底面![]() 是梯形,AB∥CD,
是梯形,AB∥CD,![]() ,AB=PD=4,CD=2,
,AB=PD=4,CD=2,![]() ,M為CD的中點,N為PB上一點,且
,M為CD的中點,N為PB上一點,且![]() .
.
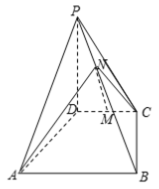
(1)若![]() MN∥平面PAD;
MN∥平面PAD;
(2)若直線AN與平面PBC所成角的正弦值為![]() ,求異面直線AD與直線CN所成角的余弦值.
,求異面直線AD與直線CN所成角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com