
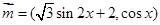 ,
,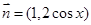 ,設函數
,設函數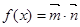 ,
,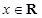 .
.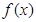 的最小正周期與最大值;
的最小正周期與最大值;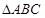 中,
中,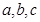 分別是角
分別是角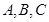 的對邊,若
的對邊,若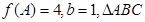 的面積為
的面積為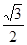 ,求
,求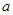 的值.
的值.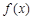 的最小正周期為
的最小正周期為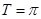 ,
,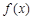 的最大值為5;(Ⅱ)
的最大值為5;(Ⅱ)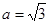 .
.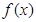 的最小正周期與最大值,首先須求出
的最小正周期與最大值,首先須求出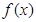 的解析式,由已知向量
的解析式,由已知向量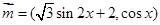 ,
,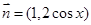 ,函數
,函數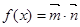 ,可將
,可將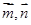 代入,根據數量積求得
代入,根據數量積求得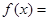
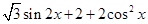 ,進行三角恒等變化,像這一類題,求周期與最大值問題,常常采用把它化成一個角的一個三角函數,即化成
,進行三角恒等變化,像這一類題,求周期與最大值問題,常常采用把它化成一個角的一個三角函數,即化成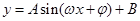 ,利用它的圖象與性質,,求出周期與最大值,本題利用兩角和與差的三角函數公式整理成
,利用它的圖象與性質,,求出周期與最大值,本題利用兩角和與差的三角函數公式整理成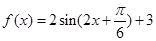 ,從而求得
,從而求得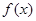 的最小正周期與最大值;(Ⅱ)在
的最小正周期與最大值;(Ⅱ)在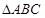 中,
中,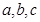 分別是角
分別是角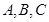 的對邊,若
的對邊,若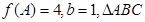 的面積為
的面積為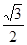 ,求
,求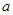 的值,要求
的值,要求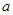 的值,一般用正弦定理或余弦定理,本題注意到
的值,一般用正弦定理或余弦定理,本題注意到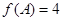 ,由
,由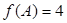 得,可求出角A的值,由已知
得,可求出角A的值,由已知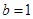 ,
,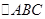 的面積為
的面積為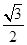 ,可利用面積公式
,可利用面積公式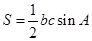 ,求出
,求出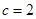 ,已知兩邊及夾角,可利用余弦定理求出
,已知兩邊及夾角,可利用余弦定理求出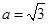 ,解此類題,主要分清邊角關系即可,一般不難.
,解此類題,主要分清邊角關系即可,一般不難.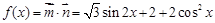
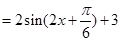 ,∴
,∴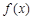 的最小正周期為
的最小正周期為 ,
,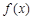 的最大值為5.
的最大值為5.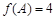 得,
得,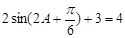 ,即
,即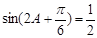 ,∵
,∵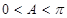 ,∴
,∴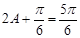 ,
,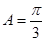 ,又
,又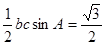 ,即
,即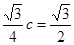 ,
,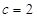 ,由余弦定理得,
,由余弦定理得,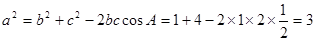


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com