
【題目】在直角坐標系xOy中,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C1的極坐標方程為ρsinθ=2.
(1)M為曲線C1上的動點,點P在線段OM上,且滿足![]() ,求點P的軌跡C2的直角坐標方程;
,求點P的軌跡C2的直角坐標方程;
(2)曲線C2上兩點![]() 與點B(ρ2,α),求△OAB面積的最大值.
與點B(ρ2,α),求△OAB面積的最大值.
【答案】(1)x2+(y﹣1)2=1(y≠0).(2)![]() .
.
【解析】
(1)設出![]() 的極坐標,然后由題意得出極坐標方程,最后轉化為直角坐標方程為
的極坐標,然后由題意得出極坐標方程,最后轉化為直角坐標方程為![]() ;
;
(2)利用(1)中的結論,設出點的極坐標,然后結合面積公式得到面積的三角函數,結合三角函數的性質可得![]() 面積的最大值為
面積的最大值為![]() .
.
解:(1)設P的極坐標為(ρ,θ)(ρ>0),M的極坐標為(ρ0,θ)(ρ0>0).
由題設知|PO|=ρ,![]() .
.
由![]() 4,
4,
得![]() ,
,
所以C2的極坐標方程ρ=2sinθ(ρ>0),
因此C2的直角坐標方程為x2+(y﹣1)2=1(y≠0).
(2)依題意:![]() ,|OB|=ρ2=2sinα.
,|OB|=ρ2=2sinα.
于是△OAB面積:S![]() .
.
當![]() 時,S取得最大值
時,S取得最大值![]() .
.
所以△OAB面積的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】千百年來,我國勞動人民在生產實踐中根據云的形狀、走向、速度、厚度、顏色等的變化,總結了豐富的“看云識天氣”的經驗,并將這些經驗編成諺語,如“天上鉤鉤云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同學為了驗證“日落云里走,雨在半夜后”,觀察了所在地區A的100天日落和夜晚天氣,得到如下![]() 列聯表:
列聯表:
夜晚天氣 日落云里走 | 下雨 | 未下雨 |
出現 | 25 | 5 |
未出現 | 25 | 45 |
臨界值表 | ||||
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
并計算得到![]() ,下列小波對地區A天氣判斷不正確的是( )
,下列小波對地區A天氣判斷不正確的是( )
A.夜晚下雨的概率約為![]()
B.未出現“日落云里走”夜晚下雨的概率約為![]()
C.有![]() 的把握認為“‘日落云里走’是否出現”與“當晚是否下雨”有關
的把握認為“‘日落云里走’是否出現”與“當晚是否下雨”有關
D.出現“日落云里走”,有![]() 的把握認為夜晚會下雨
的把握認為夜晚會下雨
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和Sn=n2+pn,且a4,a7,a12成等比數列.
(1)求數列{an}的通項公式;
(2)若bn![]() ,求數列{bn}的前n項和Tn.
,求數列{bn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .
.
(1)求證:數列![]() 為等比數列;
為等比數列;
(2)設數列![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() 為定值;
為定值;
(3)判斷數列![]() 中是否存在三項成等差數列,并證明你的結論.
中是否存在三項成等差數列,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校舉辦的體育節設有投籃項目.該項目規定:每位同學僅有三次投籃機會,其中前兩次投籃每投中一次得1分,第三次投籃投中得2分,若不中不得分,投完三次后累計總分.
(1)若甲同學每次投籃命中的概率為![]() ,且相互不影響,記甲同學投完三次后的總分為X,求隨機變量X的概率分布列;
,且相互不影響,記甲同學投完三次后的總分為X,求隨機變量X的概率分布列;
(2)若(1)中的甲同學邀請乙同學一起參加投籃項目,已知乙同學每次投籃命中的概率為![]() ,且相互不影響,甲、乙兩人之間互不干擾.求甲同學的總分低于乙同學的總分的概率.
,且相互不影響,甲、乙兩人之間互不干擾.求甲同學的總分低于乙同學的總分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在邊長為4的正三角形![]() 中,E為邊
中,E為邊![]() 的中點,過E作
的中點,過E作![]() 于D.把
于D.把![]() 沿
沿![]() 翻折至
翻折至![]() 的位置,連結
的位置,連結![]() .翻折過程中,其中正確的結論是( )
.翻折過程中,其中正確的結論是( )
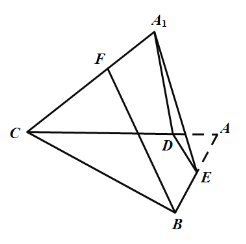
A.![]() ;
;
B.存在某個位置,使![]() ;
;
C.若![]() ,則
,則![]() 的長是定值;
的長是定值;
D.若![]() ,則四面體
,則四面體![]() 的體積最大值為
的體積最大值為![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com