
設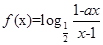 為奇函數,
為奇函數,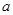 為常數,
為常數,
(1)求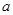 的值;
的值;
(2)證明 在區間
在區間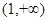 上單調遞增;
上單調遞增;
(3)若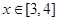 ,不等式
,不等式 恒成立,求實數
恒成立,求實數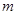 的取值范圍。
的取值范圍。
科目:高中數學 來源: 題型:解答題
已知函數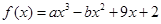 ,若f(x)在x=1處的切線方程為3x+y-6=0
,若f(x)在x=1處的切線方程為3x+y-6=0
(Ⅰ)求函數f(x)的解析式;
(Ⅱ)若對任意的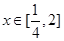 ,都有f(x)
,都有f(x)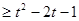 成立,求函數g(t)
成立,求函數g(t)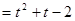 的最值
的最值
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知m∈R,對p:x1和x2是方程x2-ax-2=0的兩個根,不等式|m-5|≤|x1-x2|對任意實數a∈[1,2]恒成立;q:函數f(x)=3x2+2mx+m+ 有兩個不同的零點.求使“p且q”為假命題、“p或q”為真命題的實數m的取值范圍.
有兩個不同的零點.求使“p且q”為假命題、“p或q”為真命題的實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某地區注重生態環境建設,每年用于改造生態環境總費用為 億元,其中用于風景區改造為
億元,其中用于風景區改造為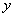 億元。該市決定建立生態環境改造投資方案,該方案要求同時具備下列三個條件:①每年用于風景區改造費用隨每年改造生態環境總費用增加而增加;②每年改造生態環境總費用至少
億元。該市決定建立生態環境改造投資方案,該方案要求同時具備下列三個條件:①每年用于風景區改造費用隨每年改造生態環境總費用增加而增加;②每年改造生態環境總費用至少 億元,至多
億元,至多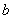 億元;③每年用于風景區改造費用不得低于每年改造生態環境總費用的15%,但不得每年改造生態環境總費用的22%。
億元;③每年用于風景區改造費用不得低于每年改造生態環境總費用的15%,但不得每年改造生態環境總費用的22%。
(1)若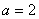 ,
,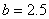 ,請你分析能否采用函數模型y=
,請你分析能否采用函數模型y=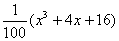 作為生態環境改造投資方案;
作為生態環境改造投資方案;
(2)若 、
、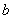 取正整數,并用函數模型y=
取正整數,并用函數模型y=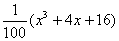 作為生態環境改造投資方案,請你求出
作為生態環境改造投資方案,請你求出 、
、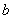 的取值.
的取值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
石家莊市為鼓勵居民節約用電,采用分段計費的方法計算電費,每月用電不超過100度時,按每度0.52元計算,每月用電量超過100度時,其中的100度仍按原標準收費,超過的部分每度按0.6元計算.
(1)設月用電 度時,應繳電費
度時,應繳電費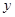 元,寫出
元,寫出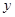 關于
關于 的函數關系式;
的函數關系式;
(2)小明家第一季度繳納電費情況如下:
| 月份 | 一月 | 二月 | 三月 | 合計 |
| 繳費金額 | 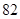 元 元 | 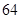 元 元 | 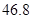 元 元 | 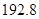 元 元 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一邊長為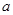 的正方形鐵片,鐵片的四角截去四個邊長均為
的正方形鐵片,鐵片的四角截去四個邊長均為 的小正方形,然后做成一個無蓋方盒。
的小正方形,然后做成一個無蓋方盒。
(1)試把方盒的容積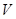 表示為
表示為 的函數;(2)
的函數;(2) 多大時,方盒的容積
多大時,方盒的容積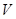 最大?
最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com