Question

在數列{a_n}中，a_n＝4n－，a₁＋a₂＋…＋a_n＝An²＋Bn，n∈N_＋，其中A，B為常數，則AB＝__________.

Answer 1

－1

解析試題分析：解法一：根據所給的數列的通項，代入n=1，得到數列的首項，代入n=2，得到數列的第二項，用這兩項寫出關于a，b的方程組，解方程組即可，解法二：根據首項的值和數列的前n項之和，列出關于a，b的方程組，得到結果。解：法一：n=1時，a₁=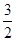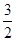，∴=a+b，①當n=2時，a₂=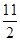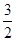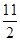，∴+=4a+2b，②，由①②得，a=2，b=-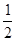，∴ab=-1．法二：a₁=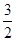，S_n=2n²-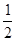n，又S_n=an²+bn，∴A=2，B=-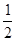，∴AB=-1．故答案為-1
考點：等差數列的基本量
點評：本題考查等差數列的基本量，考查等差數列的性質，是一個比較簡單的計算題目，在數列這一部分，基本量的運算是常見的一種題目，可難可易，伸縮性比較強．