
【題目】已知函數![]() ,
, ![]() .
.
(1)當![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 垂直時,方程
垂直時,方程![]() 有兩相異實數根,求
有兩相異實數根,求![]() 的取值范圍;
的取值范圍;
(2)若冪函數![]() 的圖象關于
的圖象關于![]() 軸對稱,求使不等式
軸對稱,求使不等式![]() 在
在![]() 上恒成立的
上恒成立的![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(1)方程![]() 有兩相異實數根等價于
有兩相異實數根等價于![]() 有兩個零點;(2)令
有兩個零點;(2)令![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,即求
上恒成立,即求![]() 的最小值
的最小值![]() ,
,
![]() ,對a分類討論研究函數的單調性,從而確定出函數的最值.
,對a分類討論研究函數的單調性,從而確定出函數的最值.
試題解析:
(Ⅰ)由題設可得![]() ,令
,令![]() ,
,
則![]() 令
令![]() 得
得![]() ,
,
|
|
|
|
|
| 0 |
|
| 遞減 | 極小值 | 遞增 |
![]() ,
,
且![]() 有兩個不等實根
有兩個不等實根![]() 即
即![]()
![]() .
.
(Ⅱ)由題設有![]() ,令
,令![]() ,
,
則![]() ,令
,令![]() ,則
,則
![]() 又
又![]() ,
, ![]() ,
, ![]() 在
在![]() 在單調遞增,
在單調遞增,
又![]() ,
,
當![]() ,即
,即![]() 時,
時, ![]() ,
,
所以![]() 在
在![]() 內單調遞增,
內單調遞增, ![]() ,所以
,所以![]() .
.
②當![]() ,即
,即![]() 時,由
時,由![]() 在
在![]() 內單調遞增,
內單調遞增,
且![]() ,
,
![]() 使得
使得![]() ,
,
|
|
|
|
|
| 0 |
|
| 遞減 | 極小值 | 遞增 |
所以![]() 的最小值為
的最小值為![]() ,
,
又![]() ,所以
,所以![]()
![]() ,
,
因此,要使當![]() 時,
時, ![]() 恒成立,只需
恒成立,只需![]() ,即
,即![]() 即可.
即可.
解得![]() ,此時由
,此時由![]() ,可得
,可得![]() .
.
以下求出a的取值范圍.
設![]() ,
, ![]() , 得
, 得![]() ,
,
所以![]() 在
在![]() 上單調遞減,從而
上單調遞減,從而![]() ,
,
綜上①②所述, ![]() 的取值范圍
的取值范圍![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() 的一條對稱軸為
的一條對稱軸為![]() ,且最高點的縱坐標是
,且最高點的縱坐標是![]() .
.
(1)求![]() 的最小值及此時函數
的最小值及此時函數![]() 的最小正周期、初相;
的最小正周期、初相;
(2)在(1)的情況下,設![]() ,求函數
,求函數![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
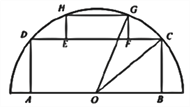
【題目】如圖,有一塊半圓形空地,開發商計劃建一個矩形游泳池![]() 及其矩形附屬設施
及其矩形附屬設施![]() ,并將剩余空地進行綠化,園林局要求綠化面積應最大化.其中半圓的圓心為
,并將剩余空地進行綠化,園林局要求綠化面積應最大化.其中半圓的圓心為![]() ,半徑為
,半徑為![]() ,矩形的一邊
,矩形的一邊![]() 在直徑上,點
在直徑上,點![]() 在圓周上,
在圓周上, ![]() 在邊
在邊![]() 上,且
上,且![]() ,設
,設![]() .
.
(1)記游泳池及其附屬設施的占地面積為![]() ,求
,求![]() 的表達式;
的表達式;
(2)當![]() 為何值時,能符合園林局的要求?
為何值時,能符合園林局的要求?
查看答案和解析>>
科目:高中數學 來源: 題型:
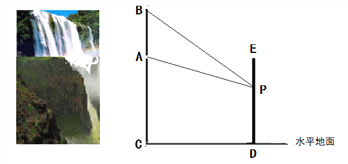
【題目】南京市江北新區計劃在一個豎直長度為20米的瀑布![]() 正前方修建一座觀光電梯
正前方修建一座觀光電梯![]() 。如圖所示,瀑布底部
。如圖所示,瀑布底部![]() 距離水平地面的高度
距離水平地面的高度![]() 為60米,電梯上設有一個安全拍照口
為60米,電梯上設有一個安全拍照口![]() ,
, ![]() 上升的最大高度為60米。設
上升的最大高度為60米。設![]() 距離水平地面的高度為
距離水平地面的高度為![]() 米,
米, ![]() 處拍照瀑布的視角
處拍照瀑布的視角![]() 為
為![]() 。攝影愛好者發現,要使照片清晰,視角
。攝影愛好者發現,要使照片清晰,視角![]() 不能小于
不能小于![]() 。
。
(1)當![]() 米時,視角
米時,視角![]() 恰好為
恰好為![]() ,求電梯和山腳的水平距離
,求電梯和山腳的水平距離![]() 。
。
(2)要使電梯拍照口![]() 的高度
的高度![]() 在52米及以上時,拍出的照片均清晰,請求出電梯和山腳的水平距離
在52米及以上時,拍出的照片均清晰,請求出電梯和山腳的水平距離![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了讓貧困地區的孩子們過一個溫暖的冬天,某校陽光志愿者社團組織“這個冬天不再冷”冬衣募捐活動,共有50名志愿者參與.志愿者的工作內容有兩項:①到各班做宣傳,倡議同學們積極捐獻冬衣;②整理、打包募捐上來的衣物.每位志愿者根據自身實際情況,只參與其中的某一項工作.相關統計數據如下表所示:

(1)如果用分層抽樣的方法從參與兩項工作的志愿者中抽取5人,再從這5人中選2人,那么“至少有1人是參與班級宣傳的志愿者”的概率是多少?
(2)若參與班級宣傳的志愿者中有12名男生,8名女生,從中選出2名志愿者,用![]() 表示所選志愿者中的女生人數,寫出隨機變量
表示所選志愿者中的女生人數,寫出隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com