Question

【題目】設函數f（x）=sin（ ﹣ ）﹣2cos2 +1． （Ⅰ）求f（x）的最小正周期；
（Ⅱ）若函數y=g（x）與y=f（x）的圖象關于直線x=1對稱，求當x∈[0， ]時y=g（x）的最大值．

Answer 1

【答案】解：（Ⅰ）化簡可得 x = sin（ ），
∴f（x）的最小正周期為 ；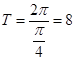
（Ⅱ）在y=g（x）的圖象上任取一點（x，g（x）），
則它關于x=1的對稱點（2﹣x，g（x））在y=f（x）的圖象上，
∴g（x）=f（2﹣x）= sin[ （2﹣x）﹣ ]
= sin（ ﹣ x﹣ ）= cos（ x+ ）
當 時， ，
∴y=g（x）在區間 上的最大值為
【解析】（Ⅰ）化簡可得f（x）= sin（ ），由周期公式可得；（Ⅱ）在y=g（x）的圖象上任取一點（x，g（x）），則它關于x=1的對稱點（2﹣x，g（x））在y=f（x）的圖象上，可得g（x）=f（2﹣x）= cos（ x+ ），由 結合余弦函數的單調性可得．