Question

【題目】如圖，在△ABC中，D為邊BC上一點，AD＝6，BD＝3，DC＝2．

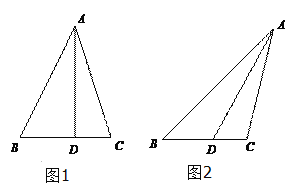
（1）若AD⊥BC，求∠BAC的大小；

（2）若∠ABC＝，求△ADC的面積．

Answer 1

【答案】（1）∠BAC＝．（2） (1＋)

【解析】 試題分析：（1）設，可得，即可求解的值，得到結論；

（2）設，得，在中，由正弦定理，得出，進而得到的值，利用兩角和的正弦函數，即可求解結論。

試題解析：

（1）設∠BAD＝α，∠DAC＝β．

因為AD⊥BC，AD＝6，BD＝3，DC＝2，

所以tanα＝，tanβ＝，所以tan∠BAC＝tan(α＋β)＝＝＝1．

又∠BAC∈(0，π)，所以∠BAC＝．

（2）設∠BAD＝α．

在△ABD中，∠ABC＝，AD＝6，BD＝3．

由正弦定理得＝， 解得sinα＝．

因為AD＞BD，所以α為銳角，從而cosα＝＝．

因此sin∠ADC＝sin(α＋)＝sinαcos＋cosαsin

＝ (＋)＝．

△ADC的面積S＝×AD×DC·sin∠ADC

＝×6×2×＝ (1＋)．