
【題目】北京市環境保護監測中心每月向公眾公布北京市各區域的空氣質量狀況![]() 年1月份各區域的
年1月份各區域的![]() 濃度情況如表:
濃度情況如表:
各區域1月份![]() 濃度
濃度![]() 單位:微克
單位:微克![]() 立方米
立方米![]() 表
表
區域 |
| 區域 |
| 區域 |
|
懷柔 | 27 | 海淀 | 34 | 平谷 | 40 |
密云 | 31 | 延慶 | 35 | 豐臺 | 42 |
門頭溝 | 32 | 西城 | 35 | 大興 | 46 |
順義 | 32 | 東城 | 36 | 開發區 | 46 |
昌平 | 32 | 石景山 | 37 | 房山 | 47 |
朝陽 | 34 | 通州 | 39 |
從上述表格隨機選擇一個區域,其2018年1月份![]() 的濃度小于36微克
的濃度小于36微克![]() 立方米的概率是
立方米的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中數學 來源: 題型:
【題目】若命題p:從有2件正品和2件次品的產品中任選2件得到都是正品的概率為三分之一;命題q:在邊長為4的正方形ABCD內任取一點M,則∠AMB>90°的概率為 ![]() ,則下列命題是真命題的是( )
,則下列命題是真命題的是( )
A.p∧q
B.(p)∧q
C.p∧(q)
D.q
查看答案和解析>>
科目:高中數學 來源: 題型:
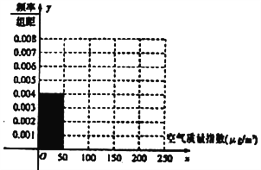
【題目】全世界越來越關注環境保護問題,某監測站點于2018年1月某日起連續![]() 天監測空氣質量指數(
天監測空氣質量指數(![]() ),數據統計如下:
),數據統計如下:
空氣質量指數( |
|
|
|
|
|
空氣質量等級 | 空氣優 | 空氣良 | 輕度污染 | 中度污染 | 重度污染 |
天數 | 20 | 40 |
| 10 | 5 |
(1)根據所給統計表和頻率分布直方圖中的信息求出![]() ,
,![]() 的值,并完成頻率分布直方圖;
的值,并完成頻率分布直方圖;
(2)由頻率分布直方圖,求該組數據的眾數和中位數;
(3)在空氣質量指數分別屬于![]() 和
和![]() 的監測數據中,用分層抽樣的方法抽取
的監測數據中,用分層抽樣的方法抽取![]() 天,再從中任意選取
天,再從中任意選取![]() 天,求事件
天,求事件![]() “兩天空氣都為良”發生的概率.
“兩天空氣都為良”發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|cosx|sinx,給出下列五個說法:
①f( ![]() π)=﹣
π)=﹣ ![]() ;
;
②若|f(x1)|=|f(x2)|,則x1=x2+kπ(k∈Z);
③f(x)在區間[﹣ ![]() ,
, ![]() ]上單調遞增;
]上單調遞增;
④函數f(x)的周期為π.
⑤f(x)的圖象關于點( ![]() ,0)成中心對稱.
,0)成中心對稱.
其中正確說法的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】種植于道路兩側、為車輛和行人遮陰并構成街景的喬木稱為行道樹![]() 為確保行人、車輛和臨近道路附屬設施安全,樹木與原有電力線之間的距離不能超出安全距離
為確保行人、車輛和臨近道路附屬設施安全,樹木與原有電力線之間的距離不能超出安全距離![]() 按照北京市
按照北京市![]() 行道樹修剪規范
行道樹修剪規范![]() 要求,當樹木與原有電力線發生矛盾時,應及時修剪樹枝
要求,當樹木與原有電力線發生矛盾時,應及時修剪樹枝![]() 行道樹修剪規范
行道樹修剪規范![]() 中規定,樹木與原有電力線的安全距離如表所示:樹木與電力線的安全距離表
中規定,樹木與原有電力線的安全距離如表所示:樹木與電力線的安全距離表
電力線 | 安全距離 | |
水平距離 | 垂直距離 | |
|
|
|
|
|
|
|
|
|
|
|
|
330KV |
|
|
500KV |
|
|
現有某棵行道樹已經自然生長2年,高度為![]() 據研究,這種行道樹自然生長的時間
據研究,這種行道樹自然生長的時間![]() 年
年![]() 與它的高度
與它的高度![]() 滿足關系式
滿足關系式![]()
![]() 1
1![]() ______;
______;![]() 將結果直接填寫在答題卡的相應位置上
將結果直接填寫在答題卡的相應位置上![]()
![]() 2
2![]() 如果這棵行道樹的正上方有35kV的電力線,該電力線距地面
如果這棵行道樹的正上方有35kV的電力線,該電力線距地面![]() 那么這棵行道樹自然生長多少年必須修剪?
那么這棵行道樹自然生長多少年必須修剪?
![]() 3
3![]() 假如這棵行道樹的正上方有500KV的電力線,這棵行道樹一直自然生長,始終不會影響電力線段安全,那么該電力線距離地面至少多少米?
假如這棵行道樹的正上方有500KV的電力線,這棵行道樹一直自然生長,始終不會影響電力線段安全,那么該電力線距離地面至少多少米?
查看答案和解析>>
科目:高中數學 來源: 題型:
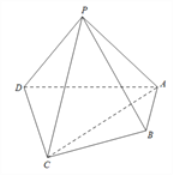
【題目】如圖,在四棱錐![]() 中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,
中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2, ![]() .
.
(1)求證:PD⊥平面PAB;
(2)求直線PB與平面PCD所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率是
的離心率是![]() ,點
,點![]() 在橢圓上,A,B分別為橢圓的右頂點與上頂點,過點A,B引橢圓C的兩條弦AE、BF交橢圓于點E,F.
在橢圓上,A,B分別為橢圓的右頂點與上頂點,過點A,B引橢圓C的兩條弦AE、BF交橢圓于點E,F.
![]() 求橢圓C的方程;
求橢圓C的方程;
![]() 若直線AE,BF的斜率互為相反數,
若直線AE,BF的斜率互為相反數,
![]() 求出直線EF的斜率;
求出直線EF的斜率;
![]() 若O為直角坐標原點,求
若O為直角坐標原點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com